chapter three
3 The DeepSeek breakthrough: Multi-Head Latent Attention (MLA)
This chapter covers
- Compressing the KV Cache with Multi-Head Latent Attention (MLA)
- Injecting positional awareness with Rotary Positional Encoding (RoPE)
- Fusing MLA and RoPE with a decoupled architecture
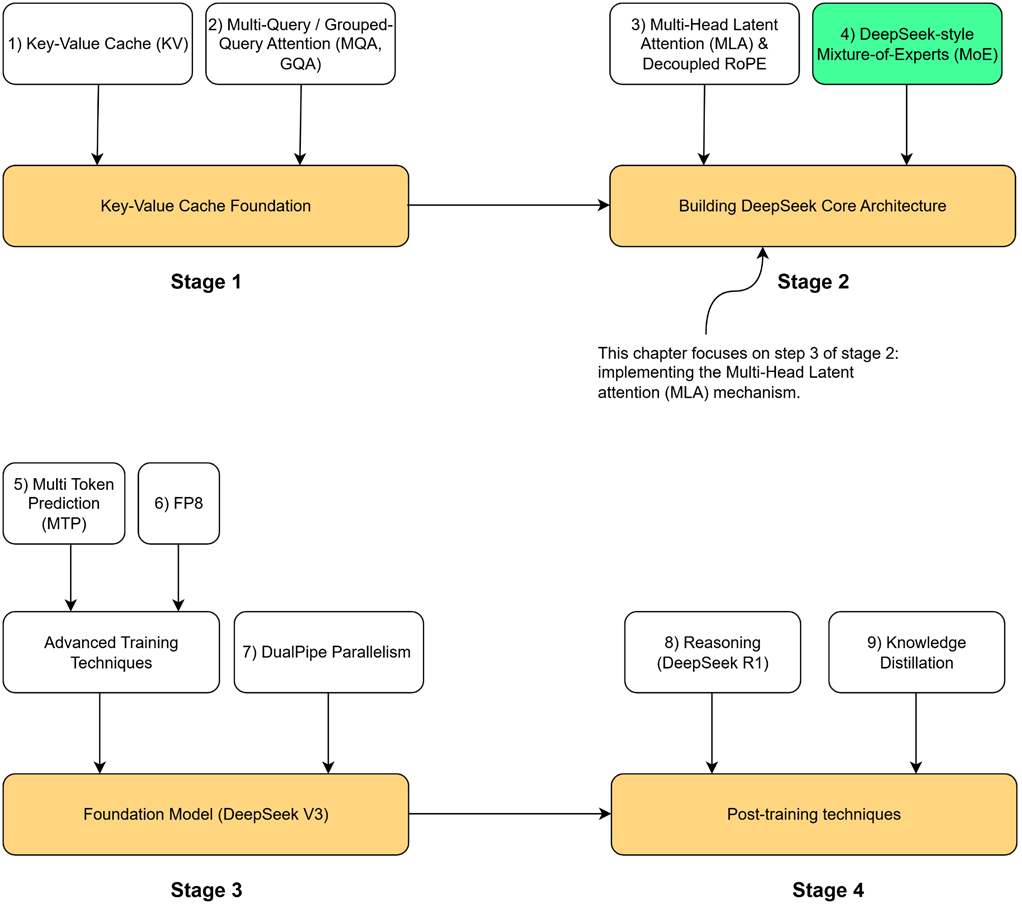
In our last chapter, we completed Stage 1 of our journey by building a solid foundation in efficient LLM inference. We began with the problem of repeated calculations, which we solved with the KV Cache. However, we then saw the dark side of the KV Cache: its massive memory cost. We explored the first-generation solutions, MQA and GQA, which help with memory usage but introduce a painful trade-off by sacrificing the expressive power of Multi-Head Attention (MHA). This left us with an unresolved tension between performance and efficiency.
Figure 3.1 Our four-stage journey to build the DeepSeek model. Having completed the Key-Value Cache Foundation (Stage 1), we now begin Stage2. This chapter focuses on the highlighted component, Multi-Head Latent Attention (MLA) & Decoupled RoPE, the first major innovation in the core architecture.