chapter four
4 Mixture-of-Experts (MoE) in DeepSeek: Scaling intelligence efficiently
This chapter covers
- Mixture of Experts (MoE) and how sparsity enables efficient scaling
- A hands-on, mathematical walkthrough of the MoE layer
- DeepSeek's advanced solutions for load balancing
The idea of Mixture of Experts (MoE) is not new; its roots trace back to a seminal 1991 paper on adaptive expert systems. However, its application to large-scale language models is a more recent development, and one that DeepSeek has pushed to its notable limits. While other models like Mistral's Mixtral brought MoE into the mainstream for LLMs, DeepSeek built upon this foundation, introducing novel tricks and techniques of its own.
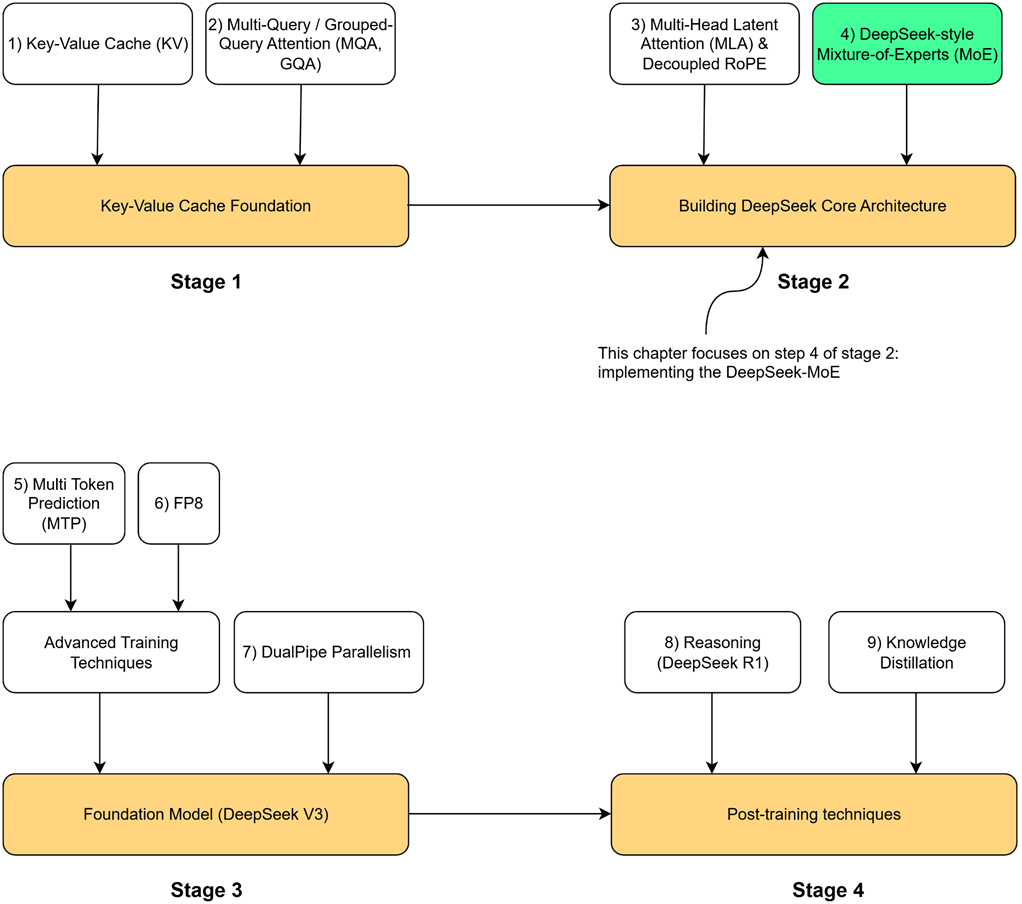
Now let’s open the black box of this mechanism. As illustrated in figure 4.1, our roadmap will cover:
- The core intuition behind MoE and the concept of sparsity.
- A detailed, mathematical, hands-on demonstration of how the MoE mechanism is implemented.
- An exploration of the critical challenge of "load balancing" and the standard solutions.
- A deep dive into the specific innovations DeepSeek introduced in their MoE architecture, from shared experts to their auxiliary-loss-free balancing.
- Finally, we will put it all
- together by coding a complete, functional MoE language model from scratch.
Figure 4.1 Our four-stage journey to build the DeepSeek model. This chapter focuses on the highlighted component, DeepSeek-style Mixture-of-Experts (MoE), the second major innovation in the core architecture.