1 Advantages and challenges of programming quantum computers
This chapter covers
- Why quantum computing is a promising tool, and what developers need to know to use it
- The main sources of quantum advantage
- High-level differences between quantum and classical computing
- An overview of the anatomy of quantum computations
Quantum computing opens the door to new ways to solve problems. For specific computational tasks, quantum computers can be much faster than traditional computers.
For some computations, the speedup is significant. One such computation is Fourier transforms, a topic we will cover in depth in chapters 7 and 8. Fourier transforms are essential for analyzing and processing signals and data in various fields such as engineering, physics, image processing, and telecommunications. Computing Fourier transforms more efficiently could enable high-frequency trading algorithms to detect market patterns faster, reducing latency in trade execution. Also, it can accelerate the filtering and compression of computer graphics.
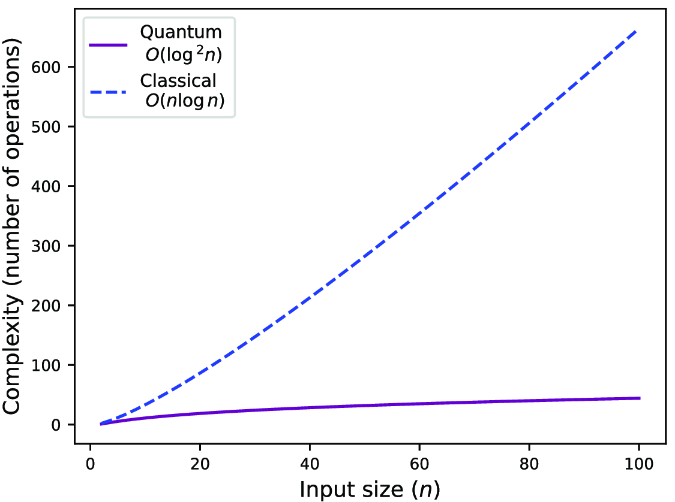
One of the best classical algorithms for computing Fourier transforms is called the fast Fourier transform (FFT), which some consider one of the most important algorithms of all time. The FFT algorithm requires exponentially more operations than its quantum implementation, as shown in figure 1.1.
Figure 1.1 Comparison of the increase in computational complexity relative to the input size for computing (fast) Fourier transforms with classical and quantum computers