3 Single-qubit state and gates
This chapter covers
- Single-qubit quantum states and an introduction to state tables
- Definitions of basic single-qubit quantum gates and an introduction to single-qubit quantum circuits
- How to simulate single-qubit quantum systems in Python
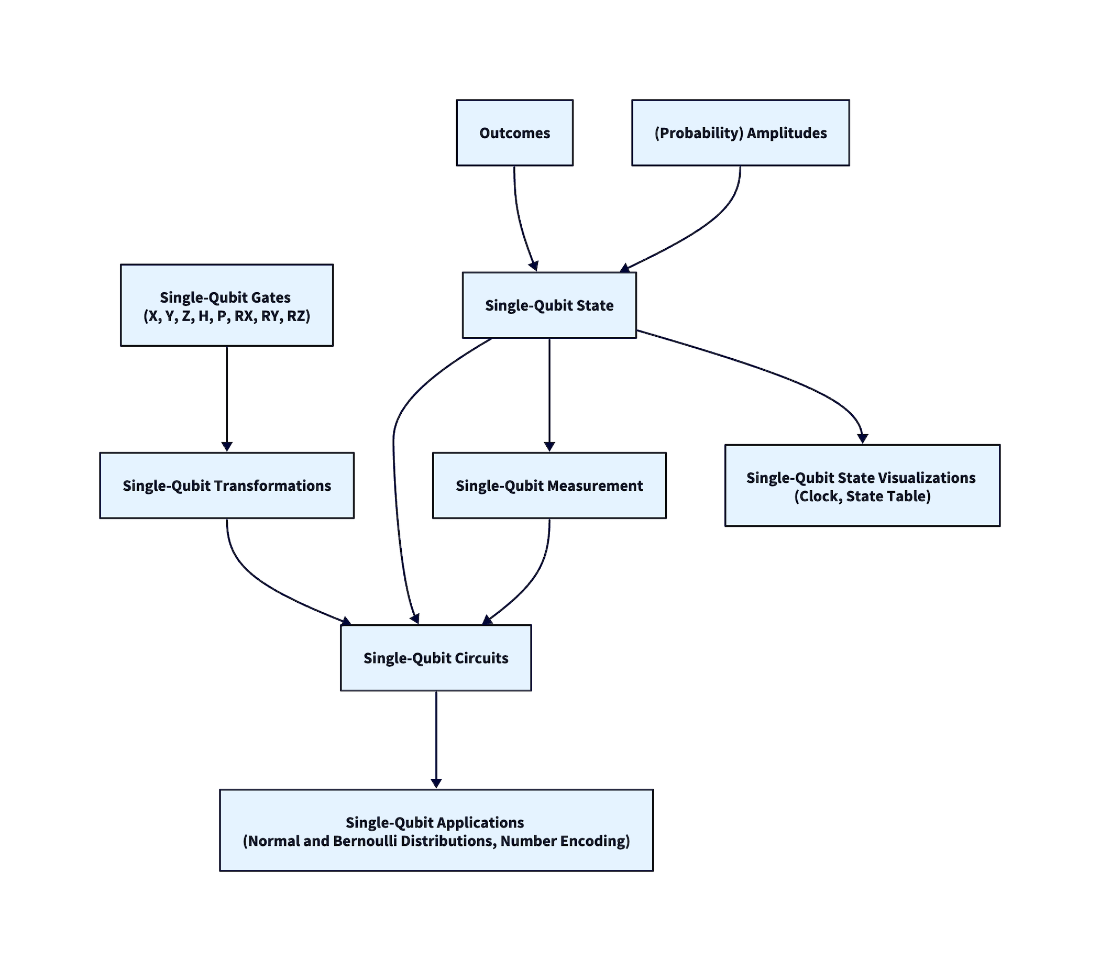
In this chapter, we look at the state of a single-qubit system with programmatic and visual representations. We cover how a qubit functions as a computational tool and how to apply quantum programming instructions. In the next chapter, we will generalize these lessons to any number of qubits.
The simplest representation of a quantum state in code is a list of complex numbers. This list is called the state vector of the quantum system used in a computation. We will use state tables, like the ones introduced in chapter 2, to visualize quantum states.
This chapter also introduces the basics of applying programming instructions, called quantum gates, to a single-qubit system, and combining them into a quantum circuit. We will look at some ways to visualize gates and circuits. Finally, we will look at a few simple single-qubit circuits with practical applications.
tip
The source code, examples, and exercise answers can be found in the book’s GitHub repository: https://learnqc.github.io/code.
Figure 3.1 Concepts introduced in this chapter.