9 Quantum phase estimation
This chapter covers
- Estimating the frequency of a periodic quantum state
- Eigenstates and eigenvalues
- Estimating the angle of rotation of a quantum circuit
- Quantum amplitude estimation and applications (quantum counting)
Now that we have learned about the QFT, we can implement one of the most useful quantum algorithms: quantum phase estimation (QPE). QPE is sometimes called the “Swiss army knife” of quantum computing. Many quantum algorithms use it as a building block. In particular, QPE plays an important role in Shor’s algorithm, a quantum computing algorithm that provides an exponential speedup over known classical algorithms for factoring integers, threatening to break the most common encryption methods used today, which involve factors of very large numbers.
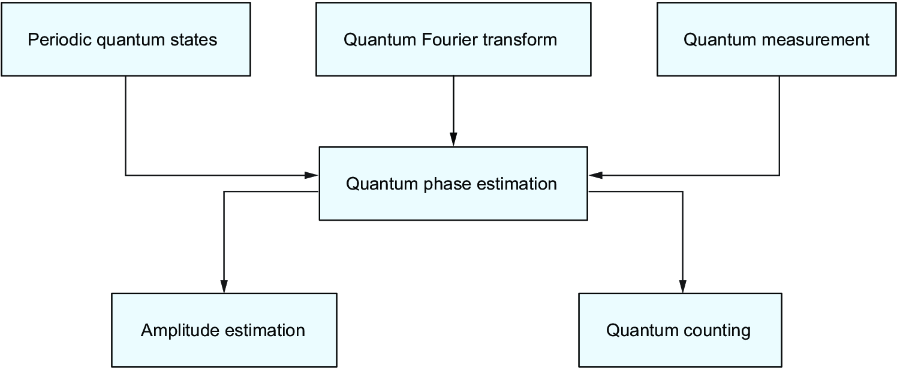
Figure 9.1 shows the concepts introduced in this chapter. First we will review periodic quantum states and how to estimate the frequency of a period quantum state with measurement. Then we will learn about QPE. Finally, we will introduce another essential algorithm, quantum amplitude estimation, and look at example applications, specifically quantum counting.
Figure 9.1 A dependency diagram of concepts covered in this chapter