appendix D Proof for doubly robust \(\widehat{ATE}_{aipw}\) estimator

 

In chapter 8, we introduced the \(\widehat{ATE}_{aipw}\) estimator and saw that it is doubly robust. If you are curious about why \(\widehat{ATE}_{aipw}\) is doubly robust, you can find the proof here. We need to check the two following conditions:

  • If the models from the T-learner are unbiased, f0(c) = E[Y|c, T = 0] and f1(c) = E[Y|c, T = 1], then \(\widehat{ATE}_{aipw}\) is also unbiased: that is, E[\(\widehat{ATE}_{aipw}\)] = ATE.
  • If the propensity score is unbiased, s(c) = P(T = 1|c), then \(\widehat{ATE}_{aipw}\) is also unbiased: that is, E[\(\widehat{ATE}_{aipw}\)] = ATE.

D.1 DR property with respect to the T-learner

We will first check the DR property for the T-learner. Assume that the models from the T-learner are unbiased. First, notice that \(\widehat{ATE}_{aipw}\) can be expressed in terms of the T-learner estimator \(\widehat{ATE}_{t}\). Consider the random variables Ti, Ci, and Yi. Then

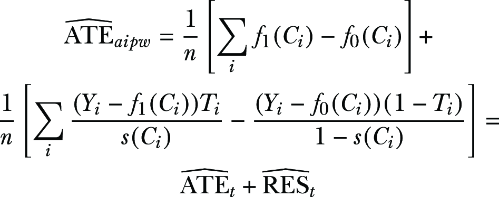
figure

If we can see that the residual has expectation zero, E[\(\widehat{RES}_{t}\)]= 0, we are done, because in that case,

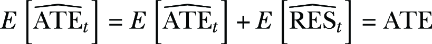
figure

Let’s see that E[\(\widehat{RES}_{t}\)]= 0. For simplicity, we will drop the index i and calculate the expectation for only one term of the summand. Using the total law of expectation, we get

(D.1)
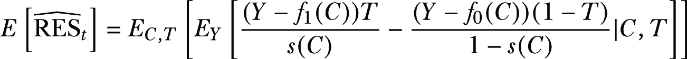
figure

Let’s start with the first term:

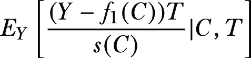
figure

When T = 0, the term cancels because T is multiplying. Assume now that T = 1.

D.2 Doubly robust property with respect to inverse probability weighting