appendix F Proof of the instrumental variable formula for imperfect compliance
In this appendix, we will prove the instrumental variable (IV) formula for imperfect compliance from chapter 10. Assume that the instrument Z and decision D are binary, and that P(D = 1|Z = 0) = 0. Then the effect of D on the outcome Y is
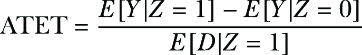
We will start with a technical result that will help us later in deriving the IV estimator. Given three random variables X, Y, Z with X and Z being binary, then for any value x = 0, 1, we have
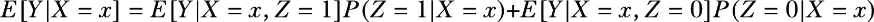
Let’s get the intuition with a simpler case, where all variables are binary and x = 1. We will mostly use the definition of conditional probability:
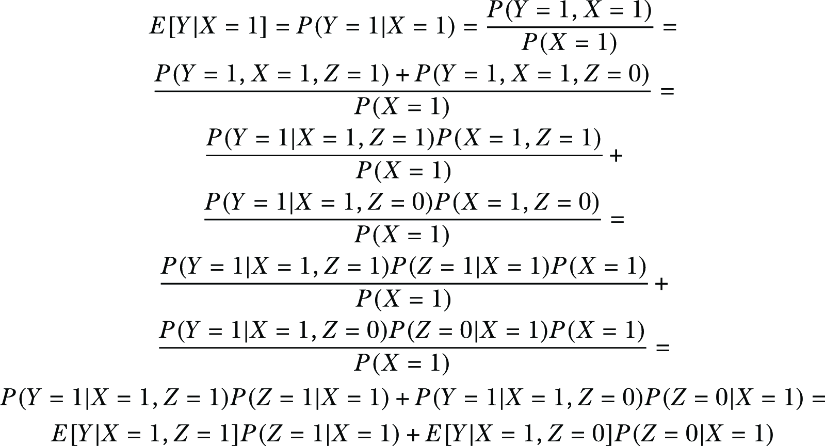
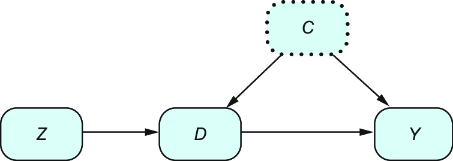
Assume we are in the IV scenario of the DAG in figure F.1 (repeated here from chapter 10 for simplicity). Also remember the consistency equation explained in chapter 10 and repeated here for convenience:
(F.1)
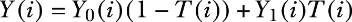
Figure F.1 General DAG for IVs
In addition, we have that there are no customers using the chatbot in the control group P(D = 1|Z = 0) = 0 (mainly because they don’t have access to it). Now we want to see that
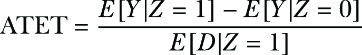
To prove this result, we need some other intermediate calculations:
- Equation F.1 can be rearranged as follows:
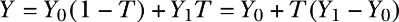
- The fact that P(D = 1|Z = 0) = 0 implies that of those who used the chatbot, all must be in the experimental group: P(Z = 0|D = 1) = 0 and P(Z = 1|D = 1) = 1.
- By the previous technical result, we have that