5 Finding comparable cases with propensity scores

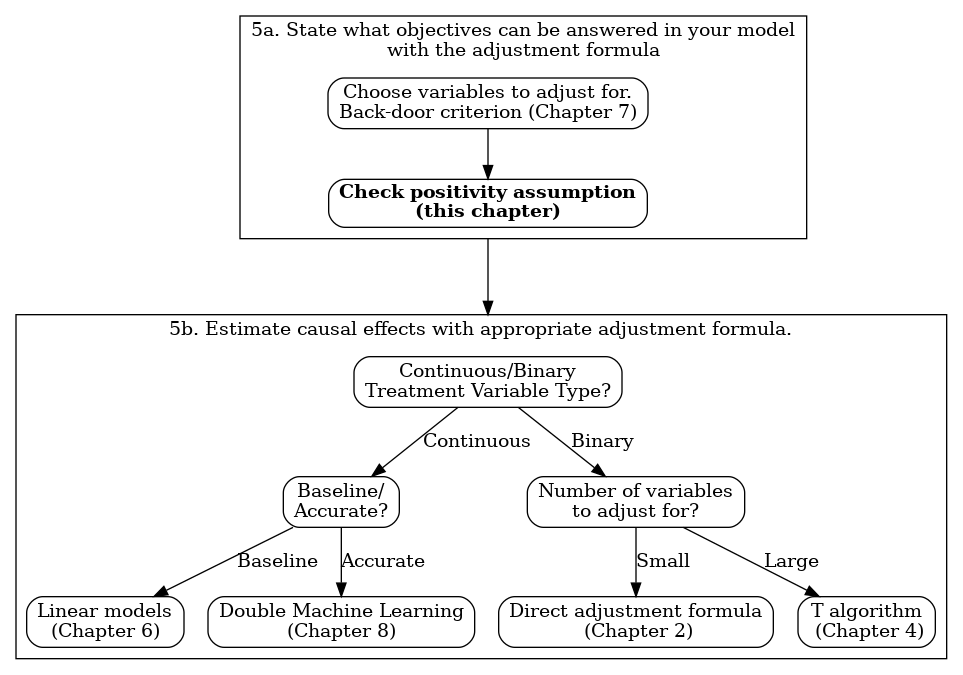
Let’s revisit the main point: how to choose between two options when we can’t use randomized controlled trials or A/B tests. Remember the kidney stones example from Chapter 2? We’ve used the adjustment formula to tackle problems like this. Now, there’s a modified version of this formula. Why do we need it? It’s specifically made to see if the positivity assumption is true or not.

Remember from Chapter 2 that the adjustment formula only works if the positivity assumption is true. Let’s go over what this assumption means. Suppose you have two treatments, A and B. You give treatment A to both young and old people, but treatment B only to young people. Now, if you want to figure out the effect of treatment B on everyone, both young and old, you hit a snag. We can’t know how treatment B affects old people unless some of them also receive this treatment. To determine which treatment is better, you need to apply both treatments, A and B, to both age groups: older and younger.

5.1 Develop your intuition about the propensity scores

5.1.1 Finding matches for estimating causal effects

5.1.2 But…​Is there a match?

5.1.3 Why matching can be hard?

5.1.4 How propensity scores can be used to calculate the ATE

5.2 Basic notions of propensity scores

5.2.1 Which cases are we working with?

5.2.2 What are the propensity scores?

5.2.3 The positivity assumption is actually…​an assumption

5.3 Propensity Scores in practice

5.3.1 Data Preparation

5.3.2 Calculate the propensity scores

5.3.3 Assess the positivity assumption

5.3.4 Calculate ATEs drawn upon the propensity scores

5.4 Calculating Propensity Score Adjustment - an exercise

5.4.1 Exercise Steps

5.5 Further reading

5.6 Chapter Quiz

5.7 Summary