chapter seven
7 Dealing with complex graphs
This chapter covers
- A mathematical definition of a causal model
- Deriving conditional independencies between variables with d-separation
- Using the back-door criterion to decide which variables to put in the adjustment formula
![[Note]](https://drek4537l1klr.cloudfront.net/ruizdevilla/v-6/Figures/note.png) Note
Note
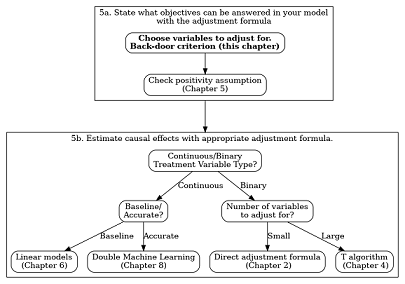
If you are wondering what you will learn regarding the adjustment formula, look at the diagram explained in Chapter 2, here as Figure 7.1. This chapter is the central core of step (5a).
We now know that one way to remove the effect of confounders is by using the adjustment formula. But in real-life DAGs, it is not always clear which variables we need to adjust for. Let’s see an example.