16 Coding kata: “Adjacency Matrix”
This coding kata covers
- Using a jagged array to represent matrices
- Implementing a doubly-linked list
- Using parallelism to calculate a matrix adjacency graph
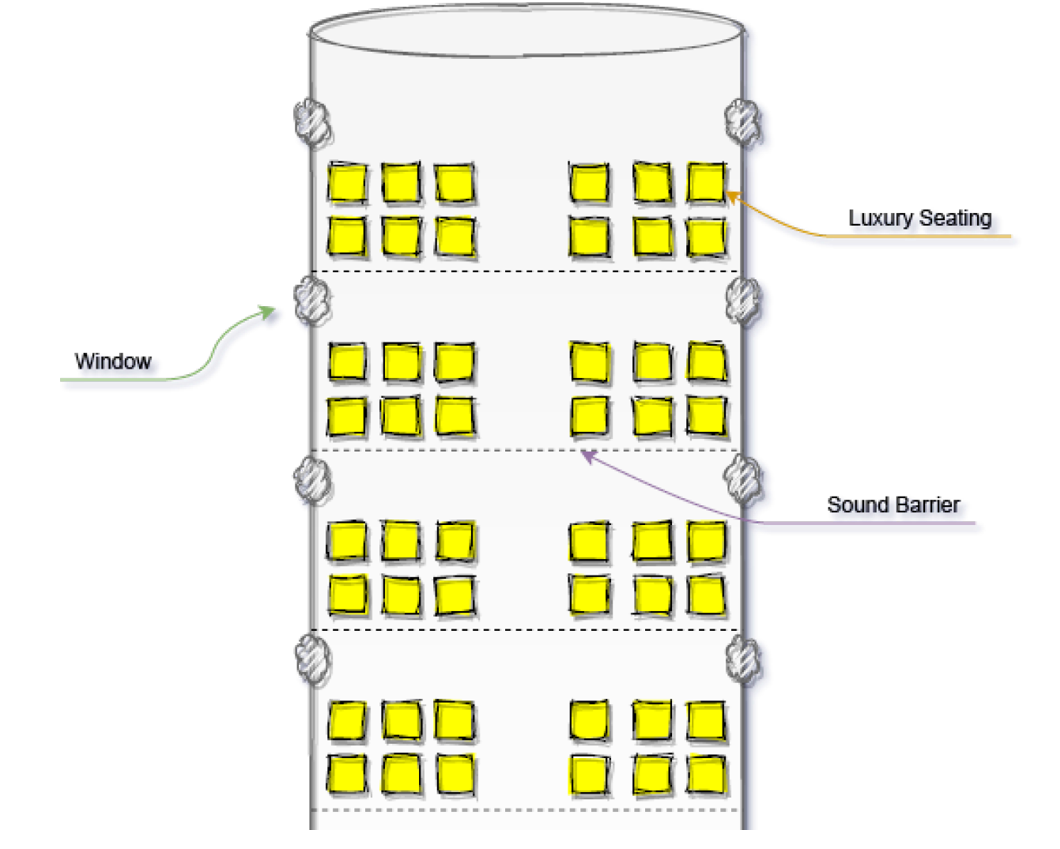
Screaming children are the bane of every sleepy passenger’s existence. Aljen van der Meulen stumbles into his office after an exhausting 30-minute flight from Cape Town to Groningen (flights are much faster in the future), complaining about the seating arrangements. Even the CEO of the airline cannot get a decent seat on a Flying Dutchman Airlines flight. To keep costs low, the airline configures all of its aircraft in a 3 by 3 seating arrangement. The rows are designed with ultimate comfort in mind, so there are only 2 rows per “block”. In every block, there are two windows for passengers to look out of (passengers do not get windows at their seats) and a sound barrier that blocks out all sounds from other blocks. There is only one class, basic economy, and the standard capacity for an airplane is 48 passengers (or 4 blocks).
Figure 16.1 All planes flying for Flying Dutchman Airlines have a 3 by 3 seating arrangement. The seats are organized in blocks of two rows, each with two windows and a sound barrier.