3 Explaining the core of elliptic curve mathematics
This chapter covers
- Elliptic curve fundamentals
- Algebra using elliptic curves
- Code for adding and multiplying points
- Embedding data on a curve
This chapter begins the journey into the mathematics of elliptic curves over finite fields. I’ll start with elliptic curves over real numbers so we can visualize what the mathematics does. Then we’ll see how elliptic curves on the complex plane map to elliptic curves over finite fields with very crude graphics. Then we’ll dive into the detailed mathematics of how we can perform addition using two points on an elliptic curve and finally expand that to the concept of multiplication.
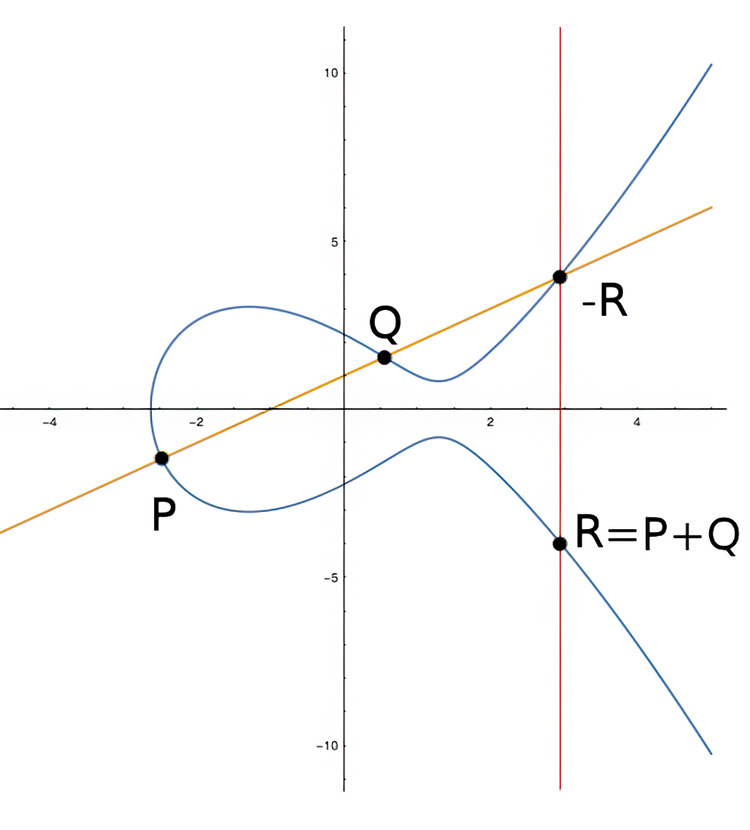
3.1 Elliptic curve algebra
In this section, I’ll describe elliptic curves in a more visual way. It is useful to keep this visualization in mind when covering elliptic curves over finite fields because the formulas are the same. The plots over finite fields are not as pretty, so there are fewer of those.
To start, I want to show the standard plot of an elliptic curve in the \((x, y)\) plane. The equation \(y^2=x^3-5 x +5\) is pretty when plotted using real numbers. Figure 3.1 shows a graph of this equation as an elliptic curve.
Figure 3.1 Elliptic curve \(y^2=x^3-5 x +5\)