Chapter 3. Designing function signatures and types
This chapter covers
- Well-designed function signatures
- Fine-grained control over the inputs to a function
- Using Option to represent the possible absence of data
The principles we’ve covered so far define functional programming in general, regardless of whether you’re programming in a statically typed language like C# or a dynamically typed language like JavaScript. In this chapter, you’ll learn some functional techniques that are specific to statically typed languages: because both the functions and their arguments are typed, this opens up a whole set of interesting considerations.
Functions are the building blocks of a functional program, so getting the function signature right is paramount. And because a function signature is defined in terms of the types of its inputs and outputs, getting those types right is just as important. Type design and function signature design are really two faces of the same coin.
You may think that, after years of defining classes and interfaces, you know how to design your types and your functions. But it turns out that FP brings a number of interesting concepts to the table that can help you increase the robustness of your programs and the usability of your APIs.
As you code more functionally, you’ll find yourself looking at the function signatures more often. Defining function signatures will be an important step in your development process, often the first thing you do as you approach a problem.
If we’re going to talk about function signatures, we’ll need some notation, so I’ll start by introducing a notation for functions that’s standard in the FP community, and we’ll use it throughout the book.
The arrow notation for expressing function signatures is very similar to notation used in languages like Haskell and F#.[1] Let’s say we have a function f from int to string; that is, it takes an int as input and yields a string as output. We’ll notate the signature like this:
1These languages have a Hindley-Milner type system (significantly different from C#’s type system), and signatures in arrow notation are called Hindley-Milner type signatures. I’m not interested in following it rigorously; instead I’ll try to make it approachable to the C# programmer.
In English, you’d read that as “f has type of int to string” or “f takes an int and yields a string.” In C#, a function with this signature is assignable to Func<int, string>.
You’ll probably agree that the arrow notation is more readable than the C# type, and that’s why we’ll use it when discussing signatures. When we have no input or no output (void), we’ll indicate this with ().
Let’s look at some examples. Table 3.1 shows function types expressed in arrow notation side by side with the corresponding C# delegate type and an example implementation of a function that has the given signature, in lambda notation.
Table 3.1. Expressing function signatures with arrow notation
| Function signature |
C# type |
Example |
|---|---|---|
| int → string | Func<int, string> | (int i) => i.ToString() |
| () → string | Func<string> | () => "hello" |
| int → () | Action<int> | (int i) => WriteLine($"gimme {i}") |
| () → () | Action | () => WriteLine("Hello World!") |
| (int, int) → int | Func<int, int, int> | (int a, int b) => a + b |
The last example in table 3.1 shows multiple input arguments: we’ll just group them with parentheses (parentheses are used to indicate tuples; that is, we’re notating a binary function as a unary function whose input argument is a binary tuple).
Now let’s move on to more complex signatures, namely those of HOFs. Let’s start with the following method (from chapter 1) that takes a string and a function from IDbConnection to R and returns an R:
How would you notate this signature? The second argument is itself a function, so it can be notated as IDbConnection → R. The HOF’s signature will be notated as follows:
And this is the corresponding C# type:
The arrow syntax is slightly more lightweight, and is more readable, especially as the complexity of the signature increases. There’s great benefit to learning it, because you’ll find it in books, articles, and blogs on FP: it’s the lingua franca used by functional programmers from different languages.
Some function signatures are more expressive than others, by which I mean that they give us more information about what the function is doing, what inputs are permissible, and what outputs we can expect. The signature () → (), for example, gives us no information at all: it may print some text, increment a counter, launch a spaceship... who knows! On the other hand, consider this signature:
Take a minute and see if you can guess what a function with this signature does. Of course, you can’t really know for sure without seeing the actual implementation, but you can make an educated guess. The function returns a list of T’s as input; it also takes a list of T’s, as well as a second argument, which is a function from T to bool: a predicate on T.
It’s reasonable to assume that the function will use the predicate on T to somehow filter the elements in the list. In short, it’s a filtering function. Indeed, this is exactly the signature of Enumerable.Where.
Let’s look at another example:
Can you guess what the function does? It returns a sequence of C’s and takes a sequence of A’s, a sequence of B’s, and a function that computes a C from an A and a B. It’s reasonable to assume that this function applies the computation to elements from the two input sequences, returning a third sequence with the computed results. This function could be the Enumerable.Zip function, which we discussed in chapter 2.
These last two signatures are so expressive that you can make a good guess at the implementation, which is, of course, a desirable trait. When you write an API, you want it to be clear, and if the signature goes hand in hand with good naming in expressing the intent of the function, all the better.
Of course, there are limits on how much a function signature can express. For instance, Enumerable.TakeWhile, a function that traverses a given sequence, yielding all elements, as long as a given predicate evaluates to true, has the same signature as Enumerable.Where. This makes sense, because TakeWhile can also be viewed as a filtering function, but one that works differently than Where.
In summary, some signatures are more expressive than others. As you develop your APIs, make your signatures as expressive as possible—this will facilitate the consumption of your API and add robustness to your programs. We’ll look at a few examples showing why as we proceed through the chapter.
Much of this chapter will focus on ways to represent the absence, or the possible absence, of data. These can seem somewhat abstract concepts, so let’s start with what happens when we actually do have some data to represent.
To represent data, we use data objects: objects that contain data, but no logic. These are also called “anemic” objects, but there’s no negative connotation in the name. In FP (unlike OOP) it’s natural to draw a separation between logic and data:
- Logic is encoded in functions.
- Data is captured with data objects, which are used as inputs and outputs to these functions.
Imagine that, in the context of a life or health insurance application, you need to write a function that calculates a customer’s risk profile, based on their age. The risk profile will be captured with an enum:
You’re pairing with a colleague who comes from a dynamically typed language, and he has a stab at implementing the function. He runs it in the REPL with a few inputs to see that it works as expected:
Although the implementation does seem to work when given reasonable inputs, you’re surprised by his choice of dynamic as the argument type, so you show him that his implementation allows client code to invoke the function with a string, causing a runtime error:
You explain to your colleague that “you can tell the compiler what type of input your function expects, so that invalid inputs can be ruled out,” and you rewrite the function, taking an int as the type of the input argument:
Is there still room for improvement?
As you keep testing your function, you find that the implementation still allows for invalid inputs:
Clearly, these are not valid values for a customer’s age. What’s a valid age, anyway? You have a word with the business to clarify this, and they indicate that a reasonable value for an age must be positive and less than 120. Your first instinct is to add some validation to your function—if the given age is outside of the valid range, throw an exception:
As you type this, you’re thinking that this is rather annoying:
- You’ll have to write additional unit tests for the cases in which validation fails.
- There are a few other areas of the application where an age is expected, so you’re probably going to need the same validation in those places. This will cause some duplication.
Duplication is usually a sign that separation of concerns has been broken: the CalculateRiskProfile function, which should only concern itself with the calculation, now also concerns itself with validation. Is there a better way?
In the meantime, another colleague, who comes from a statically typed functional language, joins the session. She looks at your code so far and finds that the problem lies in your use of int to represent age. She comments: “You can tell the compiler what type of input your function expects, so that invalid inputs can be ruled out.”
Your dynamically typed colleague listens in amazement, because those were the very words you patronized him with a few moments earlier. You’re not sure what she means exactly, so she starts to implement Age as a custom type that can only represent a valid value for an age.
In this implementation, Age still uses an int in its underlying representation, but the constructor ensures that Age can only be instantiated with a valid value.
This is functional thinking in action, because the Age type is being created precisely to represent the domain of the CalculateRiskProfile function, which can now be rewritten as follows:
This new implementation has several advantages. You’re guaranteeing that only valid values can be given; CalculateRiskProfile no longer causes runtime errors; and the concern of validating the age value is captured in the constructor of the Age type, removing the need for duplicating validation wherever an age is processed. You’re still throwing an exception in the Age constructor, but we’ll remedy that before the end of the chapter.
You can still improve things somewhat. In the preceding implementation, you’re using Value to extract the underlying value of the age, so you’re still comparing two integers. There are a couple of problems with that:
- Reading the Value property not only creates a bit of noise, it also means that you’re relying on the internal representation of Age, which you might want to change in the future.
- Because you’re performing integer comparison, you’re also not protected if, say, someone accidentally changes the hardcoded value of 60 to 600.
You can address these issues by modifying the definition of Age as follows.
Now the internal representation of an age is encapsulated, and the logic for comparison is within the Age class. You can now rewrite your function as follows:
What happens now is that a new Age will be constructed from the value 60, so that the usual validation will be applied. (If this throws a runtime error, that’s fine, because it indicates a developer error; more about this in chapter 6.) When the input age is then compared, this comparison happens in the Age class, using the comparison operators you’ve defined. Overall, the code is just as readable as before, but more robust.
In summary, primitive types are often used too liberally. If you need to constrain the inputs of your functions, it’s usually better to define a custom type. This follows the idea of making invalid state unrepresentable—in the preceding example, you can’t represent an age outside of the valid bounds.
The new implementation of CalculateRiskProfile is identical to its original implementation, except for the input type, which is now Age, and this ensures the validity of the data, as well as making the function signature more explicit. A functional programmer might say that now the function is “honest.” What does that mean?
You might hear functional programmers talk about honest or dishonest functions. An honest function is simply one that does what it says on the tin; it honors its signature—always. For instance, consider the function you ended up with:
Its signature is Age → Risk, which declares “Give me an Age and I will give you back a Risk.” Indeed, there’s no other possible outcome.[2] This function behaves as a mathematical function, mapping each element from the domain to an element of the codomain, as shown in figure 3.1.
2There is, of course, the possibility of hardware failure, of the program running out of memory, and so on, but these are not intrinsic to the function implementation.
Compare this to the previous implementation, which looked like this:
Remember, a signature is a contract. The signature int → Risk says “Give me an int (any of the 232 possible values for int) and I’ll return a Risk.” But the implementation doesn’t abide by its signature, throwing an ArgumentException for what it considers invalid input. (See figure 3.2.)
That means this function is “dishonest”—what it really should say is “Give me an int, and I may return a Risk, or I may throw an exception instead.” Sometimes there are legitimate reasons why a computation can fail, but in this example, constraining the function input so that the function always returns a valid value, is a much cleaner solution.
In summary, a function is honest if its behavior can be predicted by its signature: it returns a value of the declared type; no throwing exceptions, and no null return values. Note that these requirements are less stringent than function purity—“honesty” is an informal term, less technical and less rigorously defined than purity, but still useful.
You might require more data to fine-tune the implementation of your calculation of health risk. For instance, women statistically live longer than men, so you may want to account for this:
The signature of the function thus defined is as follows:
How many possible input values are there? Well, there are two possible values for Gender and 120 for Age, so in total there are 2 * 120 = 240 possible inputs. Notice that if you define a tuple of Age and Gender, 240 tuples are possible. The same is true if you define a custom object to hold that same data, like this:
Whether you call a binary function that accepts Age and Gender or a unary function that takes HealthData, 240 distinct inputs are possible; they’re just packaged up a bit differently.
Earlier I said that types represent sets, so the Age type represents a set of 120 elements and Gender a set of 2 elements. What about more complex types, such as HealthData, which is defined in terms of the former two?
Essentially, creating an instance of HealthData is equivalent to taking all the possible combinations of the two sets Age and Gender (a Cartesian product), and picking one element. More generally, every time you add a field to an object (or a tuple),you’re creating a Cartesian product and adding a dimension to the space of the possible values of the object, as illustrated in figure 3.3.
This concludes our brief foray into data object design. The main takeaway is that you should model objects in a way that gives you fine control over the range of inputs that your functions will need to handle. Counting the number of possible instances can bring clarity. Once you have control over these simple values, it’s easy to aggregate them into more complex data objects.
Now let’s move on to the simplest value of all: the empty tuple, or Unit.
We’ve discussed how to represent data; what about when there is no data to represent? Many functions are called for their side effects and return void. But this doesn’t play well with many functional techniques, so in this section I’ll introduce Unit: a type that can be used to represent the absence of data, without the problems of void.
Let me start by illustrating why void is less than ideal. In chapter 1 we covered the all-purpose Func and Action delegate families. But if they’re so all-purpose, why do we need two of them? Why can’t we just use Func<Void> to represent a function that returns nothing, just as we use Func<string> to represent a function that returns a string?
The problem is that although the framework has the System.Void type and the void keyword to represent “no return value,” Void receives special treatment by the compiler and can’t therefore be used as a return type (in fact, it can’t be used at all from C# code).
Let’s see why this can be a problem in practice. Say you need to gain some insight as to how long certain operations take, and to do so you write a HOF that starts a stopwatch, runs the given function, and stops the stopwatch, printing out some diagnostic information. This is a typical example of the setup/teardown scenario illustrated in chapter 1. Here’s the implementation:
If you wanted to read the contents of a file and log how long the operation took, you could use this function like this:
It would be quite natural to want to use this with a void-returning function. For example, you might want to time how long it takes to write to a file, so you’d like to write this:
The problem is that AppendAllText returns void, so it can’t be represented as a Func. To make the preceding code work, you’d need to add an overload of Instrumentation.Time that takes an Action, like this:
This is terrible! You have to duplicate the entire implementation just because of the incompatibility between the Func and Action delegates. (The same dichotomy exists in the world of asynchronous operations, between Task and Task<T>.) How can you avoid this?
If you’re going to use functional programming, it’s useful to have a different representation for “no return value.” Instead of using void, which is a special language construct, we’ll use a special value: the empty tuple. The empty tuple has no members, so it can only have one possible value; since it contains no information whatsoever, that’s as good as no value.
The empty tuple is available in the System namespace;[3] uninspiringly, it’s called ValueTuple, but I’ll follow the FP convention of calling it Unit (so called because only one value exists for this type):[4]
3Depending on what version of .NET you’re using, you may need to import the System.ValueTuple package via NuGet to make tuples available. Newer versions of each framework have (or will have) ValueTuple included in their core libraries.
4Until recently, functional libraries have tended to define their own Unit type as a struct with no members. The obvious downside is that these custom implementations aren’t compatible, so I would call for library developers to adopt the nullary ValueTuple as the standard representation for Unit.
If you have a HOF that takes a Func, but you wish to use it with an Action, how can you go about it? In chapter 1, I introduced the idea that you can write “adapter” functions to modify existing functions to suit your needs. In this case, you want a way to easily convert an Action into a Func<Unit>, and in my functional library I’ve defined ToFunc, an extension method on Action that does just that.
When you call ToFunc with a given Action, you get back a Func<Unit>: a function that, when invoked, will run the Action and return Unit.
With this in place, you can expand the Instrumentation class with a method that accepts an Action, converts it into a Func<Unit>, and calls the existing overload that works with any Func<T>.
As you can see, this enables you to avoid duplicating any logic in the implementation of Time. You must still expose the overload taking an Action, so that callers need not manually provide a function that returns Unit. Given the constraints of the language, this is the best compromise for handling both Action and Func.
While you may not be fully sold on Unit based on this example alone, you’ll see more examples in this book where Unit and ToFunc are needed to take advantage of functional techniques. In summary,
- Use void to indicate the absence of data, meaning that your function is only called for side effects and returns no information.
- Use Unit as an alternative, more flexible representation when there’s a need for consistency in the handling of Func and Action.
In this section we’ve looked at the sort of issues caused by the wide use of void, and you’ve seen how you can represent the absence of data with Unit. Next, you’ll see how to represent data that could be absent, and the much greater problems of null.
The Option type is used to represent the possibility of the absence of data, something that in C# and many other programming languages (as well as databases) is normally represented with null. I hope to show you that Option gives a more robust and expressive representation of the possible absence of data.
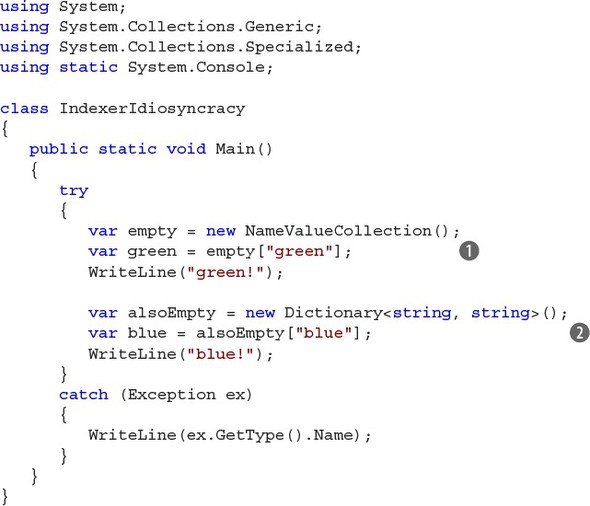
The problem of representing the possible absence of data isn’t handled very gracefully in the framework libraries. Imagine you go for a job interview and are given the following quiz:
Question: What does this program print?
Tip
NameValueCollection is a map from string to string. For example, when you call ConfigurationManager.AppSettings to get the settings of a .config file, you get a NameValueCollection.
Take a moment to read through the code. Then, write down what you think the program prints (making sure nobody’s looking). And once you’ve answered that question, how much would you be willing to bet that you got the right answer? If you’re like me, and have a nagging feeling that as a programmer you should really be concerned with other things than these annoying details, the rest of this section will help you see why the problem lies with the APIs themselves, and not with your lack of knowledge.
The code uses indexers to retrieve items from two empty collections, so both operations will fail. Indexers are, of course, just normal functions—the [] syntax is just sugar—so both indexers are functions of type string → string, and both are dishonest.
The NameValueCollection indexer  returns null if a key isn’t present. It’s somewhat open to debate whether null is actually a string, but I’d tend to say no.[5] You give the indexer a perfectly valid input string, and it returns the useless null value—not what the signature claims.
returns null if a key isn’t present. It’s somewhat open to debate whether null is actually a string, but I’d tend to say no.[5] You give the indexer a perfectly valid input string, and it returns the useless null value—not what the signature claims.
5In fact, the language specification itself says so: if you assign null to a variable, as in string s = null;, then s is string evaluates to false.
The Dictionary indexer  throws a KeyNotFoundException, so it’s a function that says “Give me a string and I’ll return you a string,” when it should actually say “give me a string and I may return you a string, or I may throw an exception instead.”
throws a KeyNotFoundException, so it’s a function that says “Give me a string and I’ll return you a string,” when it should actually say “give me a string and I may return you a string, or I may throw an exception instead.”
To add insult to injury, the two indexers are dishonest in inconsistent ways. Knowing this, it’s easy to see that the program prints the following:
That is, the interface exposed by two different associative collections in .NET is inconsistent. Who’d have thought? And the only way to find out is by looking at the documentation (boring) or stumbling on a bug (worse).
Let’s look at the functional approach to representing the possible absence of data.
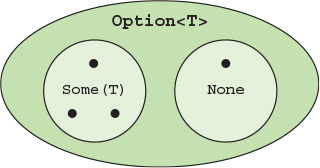
Option is essentially a container that wraps a value...or no value. It’s like a box that may contain a thing, or it could be empty. The symbolic definition for Option is as follows:
Let’s see what that means. T is a type parameter—the type of the inner value—so an Option<int> may contain an int, or not. The | sign means or, so the definition says that an Option<T> can be one of two things—or, equivalently, it can be in one of two “states”:
- None—A special value indicating the absence of a value. If the Option has no inner value, we say that “the Option is None.”
- Some(T)—A container that wraps a value of type T. If the Option has an inner value, we say that “the Option is Some.”
Option is also called Maybe
Different functional frameworks use varying terminology to express similar concepts. A common synonym for Option is Maybe, with the Some and None states called Just and Nothing respectively.
Such naming inconsistencies are unfortunately quite common in FP, and this doesn’t help in the learning process. In this book, I’ll try to present the most common synonyms for each pattern or technique, and then stick with one name.
So from now on, I’ll stick to Option; just know that if you run across Maybe—say, in a JavaScript or Haskell library—it’s the same concept.
We’ll look at implementing Option in the next subsection, but first let’s take a look at its basic usage so you’re familiar with the API. I recommend you follow along in the REPL; you’ll need a bit of setup, and that’s described in the “Using the LaYumba.Functional library in the REPL” sidebar.
Using the LaYumba.Functional library in the REPL
Playing with the constructs in the LaYumba.Functional library in the REPL requires a bit of setup:
- If you haven’t done so already, download and compile the code samples from https://github.com/la-yumba/functional-csharp-code.
- Reference the LaYumba.Functional library in your REPL. Just how this works depends on your setup. On my system (using the REPL in Visual Studio, with the code samples solution open), I can do so by typing the following:
- Type the following imports into the REPL:
Once you’re set up, you can create some Options:

That was easy! Now that you know how to create Options, how can you interact with them? At the most basic level, you can do so with Match, a method that performs pattern matching. Simply put, it allows you to run different code depending on whether the Option is None or Some.
For example, if you have an optional name, you can write a function that returns a greeting for that name, or a general-purpose message if no name is given. Type the following into the REPL:

As you can see, Match takes two functions: the first one says what to do in the None case, the second what to do in the Some case. In the Some case, the function will be given the inner value of the Option (in this case, the string "John", the value given when the Option was created).
In the preceding call to Match, the named arguments None: and Some: are used for extra clarity. It’s possible to omit those:
In general, I will omit them because the empty parens () in the first lambda already suggest an empty container (that is, an Option in the None state), whereas the parens with an argument inside, (name), suggest a container with a value inside.
If this is all a bit confusing right now, don’t worry; things will fall into place as we go along. For now, these are the things to remember:
- Use Some(value) to wrap a value into an Option.
- Use None to create an empty Option.
- Use Match to run some code depending on the state of the Option.
For now, you can think of None as a replacement for null, and Match as a replacement for a null-check. Conceptually, the preceding code is not so different from this:
You’ll see in subsequent sections why using Option is actually preferable to null, and why, eventually, you won’t need to use Match very often. First, though, let’s have a look under the hood.
You can skip this section on first reading, or if you’re only interested in understanding enough to be able to use Option. Here I’ll show you the techniques I used in the implementation of Option I included in LaYumba.Functional. This is both to show you that there’s very little magic involved, and to show possible ways to work around some limitations of the C# type system.
In many typed functional languages, Option can be defined with a one-liner along these lines:
In C#, more work is required. First, you need None and Some<T> to represent each possible state for an Option.

The F class is meant as the entry point for client code; it exposes the value None, which is the empty option, and the function Some, which will wrap a given T into a Some<T>.
None represents the absence of a value, so it’s a type with no instance fields. Just like Unit, there’s only one possible value for None. Some has a single field that holds the inner value; this can’t be null.
The preceding code allows you to explicitly create values in the None or Some state:
The next step is to define the more general Option<T> type, which could be either None or Some<T>. In terms of sets, Option<T> is the union of the set Some<T> with the singleton set None (see figure 3.4).
This turns out not to be so easy, because C# doesn’t have language support for defining such “union types.” Ideally I’d like to be able to write something like this.
That is, I’d like to say that None is an Option<T>, and so is Some<T>. Unfortunately, there are several problems with the preceding code (which, as a consequence, doesn’t compile):
- None doesn’t have (and doesn’t need) a type parameter T; it can’t therefore implement the generic interface Option<T>. It would be nice if None could be treated as an Option<T> regardless of what type the type parameter T is eventually assigned, but this isn’t supported by C#’s type system.
- An Option<T> can only be one of two things: None or Some<T>. It shouldn’t be possible for any client assembly to define any other implementations of Option<T>, but there’s no language feature to enforce this.
Given these issues, using an interface or abstract class for Option doesn’t work very well. Instead, I defined Option<T> as a separate class and defined methods so that both None and Some<T> can be implicitly converted into Option<T> (inheritance by implicit conversion, if you like).
This implementation of Option can represent both None and Some; it has a Boolean value to discriminate between these two states, as well as a field of type T to store the inner value of a Some.
You can now treat None as an Option<T> for any type T. When None is converted to an Option<T>, the isSome flag will be false; the inner value will be the default value for T and will be disregarded. When Some<T> is converted into an Option<T>, the isSome flag is true and the inner value is stored.
I also added a method to implicitly lift a value of type T into an Option<T>, which will prove convenient in some scenarios. It yields an Option in the None state if the value is null, and it wraps the value into a Some otherwise.
The most important part is Match, which allows you to run code depending on the state of the Option. Match is a method that says “Tell me what you want done when there’s no value, and what you want done when there is a value, and I’ll do whatever’s appropriate.”
With this in place, you can consume an Option. Take another look at the use of Match I showed earlier. It should be clearer now:
Note that there are many other possible ways to define an Option in C#. I’ve chosen this particular implementation because it allows the cleanest API from the perspective of client code. But Option is a concept, not a particular implementation, so don’t be alarmed if you see a different implementation in another library or tutorial.[6] It will still have the defining features of an Option:
6For example, the popular mocking framework NSubstitute includes an implementation of Option.
- A value None that indicates the absence of a value
- A function Some that wraps a value, indicating the presence of a value
- A way to execute code conditionally on whether a value is present (in our case, Match)
Next, let’s see why it’s better to use Option than null to represent the possible absence of a value.
I mentioned earlier that None should be used instead of null, and Match instead of a null-check. Let’s see what we gain by doing so with a practical example.
Imagine you have a form on your website that allows people to subscribe to a newsletter. A subscriber enters their name and email, and this causes the creation of a Subscriber instance, defined as follows, which is persisted to the database:
When it’s time to send out the newsletter, a custom greeting is computed for the subscriber, which will be prepended to the body of the newsletter:
This all works fine. Name can’t be null because it’s a required field in the signup form, and it’s not nullable in the database.
Some months later, the rate at which new subscribers sign up drops, so the business decides to lower the barrier to entry by no longer requiring new subscribers to enter their name. The name field is removed from the form, and the database is modified accordingly.
This should be considered a breaking change, because it’s not possible to make the same assumptions about the data any more. If you allow Name to be null, the code will happily compile, and GreetingFor will throw an exception when it receives a Subscriber without a Name.
By this time, the person responsible for making the name optional in the database may be on a different team than the person maintaining the code that sends out the newsletter. The code may be in different repositories. In short, it may not be simple to look up all the uses of Name.
Instead, it’s better to explicitly indicate that Name is now optional. The Subscriber class should be modified to look like this:

This not only clearly conveys the fact that a value for Name may not be available; it causes GreetingFor to no longer compile. GreetingFor, and any other code that was accessing the Name property, will have to be modified to take into account the possibility of the value being absent. For example, you might modify it like so:
By using Option, you’re forcing the users of your API to handle the case in which no data is available. This places greater demands on the client code, but it effectively removes the possibility of a NullReferenceException occurring. Changing a string to an Option<string> is a breaking change: in this way, you’re trading runtime errors for compile-time errors, thus making a compiling application more robust.
We’ve discussed how functions map elements from one set to another, and how types in typed programming languages describe such sets. There’s an important distinction to make between total and partial functions:
- Total functions are mappings that are defined for every element of the domain.
- Partial functions are mappings that are defined for some, but not all, elements of the domain.
Partial functions are problematic because it’s not clear what the function should do when given an input for which it can’t compute a result? The Option type offers a perfect solution to model such cases: if the function is defined for the given input, it returns a Some wrapping the result; otherwise, it returns None.
Let’s look at some common use cases in which we can use this approach.
Imagine a function that parses a string representation of an integer. You could model this as a function of type string → int. This is clearly a partial function because not all strings are valid representations of integers. In fact, there are infinitely many strings that can’t be mapped to an int.
You can provide a safer representation of parsing with Option, by having the parser function return an Option<int>. This will be None if the given string couldn’t be parsed, as illustrated in figure 3.5.
A parser function with the signature string → int is partial, and it’s not clear from the signature what will happen if you supply a string that can’t be converted to an int. On the other hand, a parser function with signature string → Option<int> is total, because for any given string it will return a valid Option<int>.
Here’s an implementation that uses the framework methods to do the grunt work but exposes an Option-based API:
The helper functions in this subsection are included in LaYumba.Functional, so you can try them out in the REPL:
Similar methods are defined to parse strings into other commonly used types, like doubles and dates, and, more generally, to convert data in one form to another more restrictive form.
In the opening part of this section, I showed you that the framework collections expose an API that’s neither honest nor consistent in representing the absence of data. The gist was as follows:
The fundamental problem is the following. An associative collection maps keys to values, and can therefore be seen as a function of type TKey → TValue. But there’s no guarantee that the collection contains a value for every possible key of type TKey, so looking up a value can always be a partial function.
A better, more explicit way to model the retrieval of a value is by returning an Option. It’s possible to write adapter functions that expose an Option-based API, and I generally name these Option-returning functions Lookup:
Lookup takes a NameValueCollection and a string (the key), and will return Some with the value if the key exists, and None otherwise. Here’s the implementation:
That’s it! The expression @this[key] is of type string, whereas the return value is Option<string>, so the string value will be implicitly converted into an Option<string>. (Remember, in the implementation of Option shown earlier, implicit conversion from a value T to an Option<T> was defined to return None if the value was null, and to lift the value into a Some otherwise.) We’ve gone from a null-based API to an Option-based API.
Here’s an overload of Lookup that takes an IDictionary. The signature is similar:
The Lookup function can be implemented as follows:
We now have an honest, clear, and consistent API to query both collections. When you access these collections with Lookup, the compiler forces you to handle the None case and you know exactly what to expect:
No more KeyNotFoundException or NullReferenceException because you asked for a key that wasn’t present in the collection. The same approach can be applied when querying other data structures.
Earlier in this chapter, we defined the Age type, a type more restrictive than int, that only allows the representation of a valid value for a person’s age. When creating an Age from an int, we needed to account for the possibility that the given int didn’t represent a valid age. You can again model this with Option, as shown in figure 3.6.
If you need to create an Age from an int, instead of calling the constructor (which has to throw an exception if it’s unable to create a valid instance), you can define a function that returns Some or None to indicate the successful creation of an Age. This is known as a smart constructor: it’s “smart” in the sense that it’s aware of some rules and can prevent the construction of an invalid object.
If you now need to obtain an Age from an int, you’ll get an Option<Age> instead, which forces you to account for the failure case. If your Option<Age> is None, what do you do with it? Well, that depends on the context and requirements. In upcoming chapters we’ll look at how you can work effectively with Options. Although Match is the basic way of interacting with an Option, we’ll build a rich, high-level API starting in the next chapter.
In summary, Option should be your default choice when representing a value that’s, well, optional! Use it in your data objects to model the fact that a property may not be set, and in your functions to indicate the possibility that a suitable value may not be returned. Apart from reducing the chance of a NullReferenceException, this will enrich your model and make your code more self-documenting.
Guarding against NullReferenceException
To further bulletproof your code against lurking NullReferenceExceptions, never write a function that explicitly returns null, and always check that the inputs to public methods in your APIs aren’t null.[7] The only reasonable exception for this is optional arguments, which need their default value to be a compile-time constant.
7This tedious task can be automated using PostSharp. If you’re inclined to go this way, check out NullGuard (https://github.com/haacked/NullGuard), which allows you to disallow null arguments on a per-assembly basis, giving you the best protection with the least amount of boilerplate.
Using Option in your function signature is one way you can attain the overarching recommendation of this chapter: designing function signatures that are honest and highly descriptive of what can be expected from the function. I’ve tried to show how this makes your application more robust by reducing the chances of runtime errors, but nothing beats proof by experiment, so try these ideas out in your own code.
In the next chapter, we’ll enrich the Option API. Option will be your friend, not only when you use it in your programs, but also as a simple structure through which I’ll illustrate many FP concepts.
- Write a generic function that takes a string and parses it as a value of an enum. It should be usable as follows:
- Write a Lookup function that will take an IEnumerable and a predicate, and return the first element in the IEnumerable that matches the predicate, or None if no matching element is found. Write its signature in arrow notation:
- Write a type Email that wraps an underlying string, enforcing that it’s in a valid format. Ensure that you include the following:
- A smart constructor
- Implicit conversion to string, so that it can easily be used with the typical API for sending emails
- Take a look at the extension methods defined on IEnumerable in System.LINQ.Enumerable.[8] Which ones could potentially return nothing, or throw some kind of not-found exception, and would therefore be good candidates for returning an Option<T> instead?
8See the Microsoft documentation of Enumerable Methods: https://docs.microsoft.com/en-us/dotnet/api/system.linq.enumerable
- Write implementations for the methods in the following AppConfig class. (For both methods, a reasonable one-line method body is possible. Assume the settings are of type string, numeric, or date.) Can this implementation help you to test code that relies on settings in a .config file?
- Make your function signatures as specific as possible. This will make them easier to consume and less error-prone.
- Make your functions honest. An honest function always does what its signature says, and given an input of the expected type, it yields an output of the expected type—no Exceptions, no nulls.
- Use custom types rather than ad hoc validation code to constrain the input values of a function, and use smart constructors to instantiate these types.
- Use the Option type to express the possible absence of a value. An Option can be in one of two states:
- None, indicating the absence of a value
- Some, a simple container wrapping a a non-null value
- To execute code conditionally, depending on the state of an Option, use Match with the functions you’d like to evaluate in the None and Some cases.