In this chapter
- You learn what a tree is and the difference between trees and graphs.
- You get comfortable with running an algorithm over a tree.
- You learn depth-first search and see the difference between depth-first search and breadth-first search.
- You learn Huffman coding, a compression algorithm that makes use of trees.
What do compression algorithms and database storage have in common? There is often a tree underneath doing all the hard work. Trees are a subset of graphs. They are worth covering separately as there are many specialized types of trees. For example, Huffman coding, a compression algorithm you will learn in this chapter, uses binary trees.

Most databases use a balanced tree like a B-tree, which you will learn about in the next chapter. There are so many types of trees out there. These two chapters will give you the vocabulary and concepts you need to understand them.
Trees are a type of graph. We will have a more thorough definition later. First, let’s learn some terminology and look at an example.
Just like graphs, trees are made of nodes and edges.
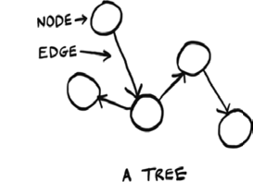
In this book, we will work with rooted trees. Rooted trees have one node that leads to all the other nodes.
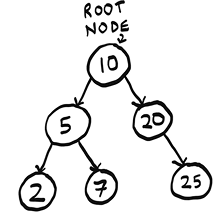
We will work exclusively with rooted trees, so when I say tree in this chapter, I mean a rooted tree. Nodes can have children, and child nodes can have a parent.
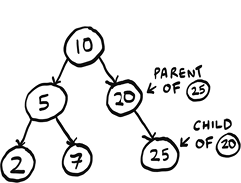
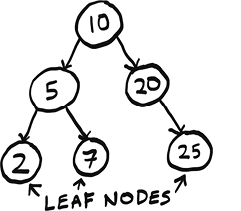
In a tree, nodes have at most one parent. The only node with no parents is the root. Nodes with no children are called leaf nodes.