In this chapter
- You learn about a new data structure called binary search trees (BSTs).
- You learn about balanced trees and why they often perform better than arrays or linked lists.
- You also learn about AVL trees, a type of balanced BST. In the worst-case scenario, binary trees can be slow. A balanced tree will help them perform effectively.
In the last chapter, you learned about the new data structure, trees. Now that you and trees are best friends, it’s time to see what they are used for. When arrays and linked lists fail to deliver the desired performance, a good next step is to try a tree. In this chapter, we’ll discuss the performance that trees can offer. We’ll then explore a special type of tree that can offer exceptional performance, called a balanced tree.

Remember binary search from way back in chapter 1? Using binary search, we are able to find information much more quickly than if we did a simple search using O(log n) instead of O(n). There is one problem, though: insertion. Sure, searching takes O(log n) time, but the array needs to be sorted. If you want to insert a new number into your sorted array, it will take O(n) time. The issue is making a spot for the new value. You need to move a bunch of values to make room.
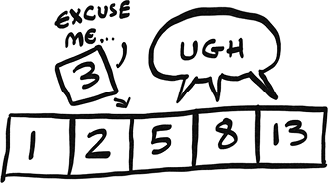
If only we could insert like we do in a linked list, where we just need to change a couple of pointers.
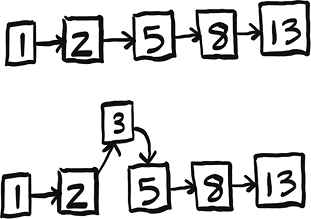
But searching is linear time in linked lists. How can we get the best of both worlds?