chapter eight
Chapter 8. Greedy algorithms

- You learn how to tackle the impossible: problems that have no fast algorithmic solution (NP-complete problems).
- You learn how to identify such problems when you see them, so you don’t waste time trying to find a fast algorithm for them.
- You learn about approximation algorithms, which you can use to find an approximate solution to an NP-complete problem quickly.
- You learn about the greedy strategy, a very simple problem-solving strategy.

Suppose you have a classroom and want to hold as many classes here as possible. You get a list of classes.
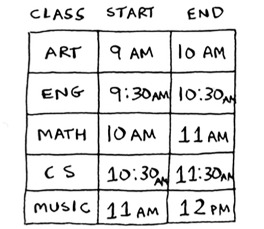
You can’t hold all of these classes in there, because some of them overlap.

You want to hold as many classes as possible in this classroom. How do you pick what set of classes to hold, so that you get the biggest set of classes possible?
Sounds like a hard problem, right? Actually, the algorithm is so easy, it might surprise you. Here’s how it works:
- Pick the class that ends the soonest. This is the first class you’ll hold in this classroom.
- Now, you have to pick a class that starts after the first class. Again, pick the class that ends the soonest. This is the second class you’ll hold.
Keep doing this, and you’ll end up with the answer! Let’s try it out. Art ends the soonest, at 10:00 a.m., so that’s one of the classes you pick.

Now you need the next class that starts after 10:00 a.m. and ends the soonest.

English is out because it conflicts with Art, but Math works.