11 Finding boundaries with style: Support vector machines and the kernel method

This chapter covers
- What is a support vector machine?
- Of all the linear classifiers for a dataset, which one has the best boundary?
- Using the kernel method to build non-linear classifiers.
- Coding support vector machines and the kernel method in sklearn.
In this chapter I teach you a very powerful classification model called the support vector machine (SVM for short). An SVM is similar to a perceptron, in that it separates a dataset with two classes using a linear boundary. However, the SVM aims to find the linear boundary that is located as far as possible from the points in the dataset. I also teach you the kernel method. The kernel method is a very useful method, which when used in conjunction with an SVM, can classify datasets using highly non-linear boundaries.
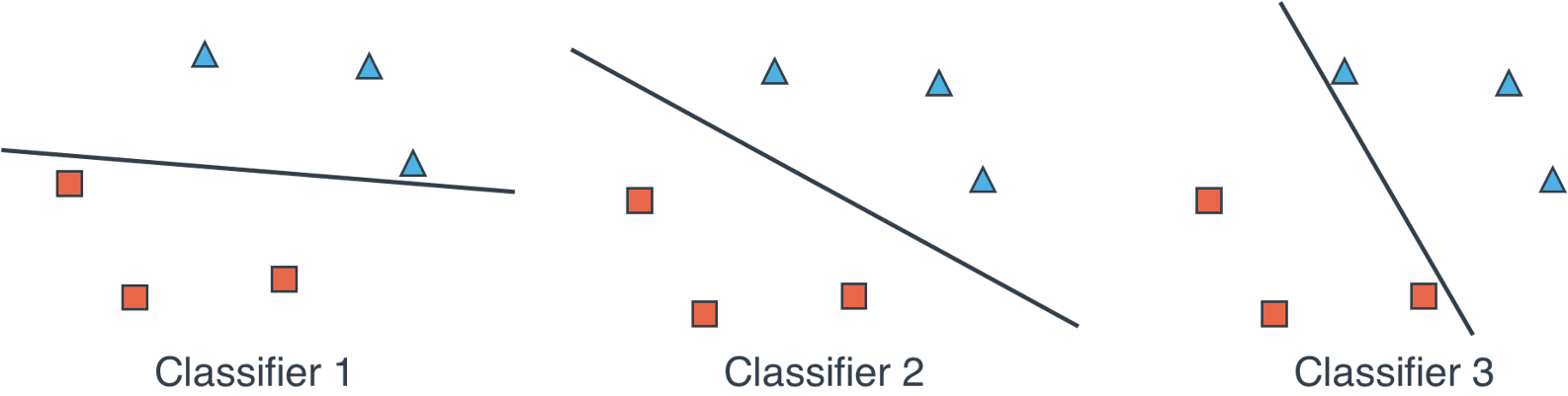
In Chapters 5 we learned linear classifiers, or perceptrons. With two-dimensional data, these are defined by a line that separates a dataset consisting of points with two labels. However, you may have noticed that many different lines can separate a dataset, and this raises the following question: How do you know which is the best line? In figure 11.1 I show you three different linear classifiers that separate this dataset. Which one do you prefer, classifier 1, 2, or 3?
Figure 11.1. Three classifiers that classify our data set correctly. Which one do you prefer, Classifier 1, 2, or 3?