chapter nine
9 Finding boundaries with style:
Support vector machines and the kernel method
This chapter covers
- What is a support vector machine?
- What does it mean for a linear classifier to fit well between the points?
- A new linear classifier which consists of two lines, and its new error function.
- Tradeoff between good classification and a good fit: the C parameter.
- Using the kernel method to build non-linear classifiers.
- Types of kernels: polynomial and radial basis function (rbf) kernel.
- Coding SVMs and the kernel method in sklearn.
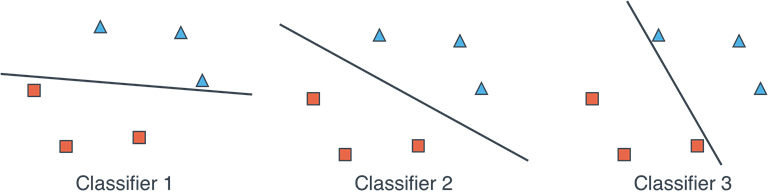
In Chapters 4 and 5, we learned about linear classifiers. In two dimensions, these are simply defined by a line that best separates a dataset of points with two labels. However, you may have noticed that many different lines can separate a dataset, and this raises the question: How do you know which is the best line? In figure 9.1 I show you three different classifiers that separate this dataset. Which one do you prefer, classifier 1, 2, or 3?
Figure 9.1. Three classifiers that classify our data set correctly. Which one do we prefer, Classifier 1, 2, or 3?