appendix B Answers to exercises

 

2.1 Derive full conditionals p(xA|xB) for multivariate Gaussian distribution, where A and B are subsets of x1, x2, ..., xn of jointly Gaussian random variables.

Let’s partition our vector x into two subsets, xA and xB, and then we can write down the mean and covariance matrices in block form:

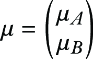
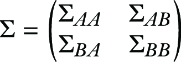
figure
figure

To compute the conditional distributions, we get the following result:

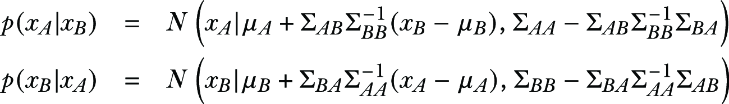
figure

2.2 Derive marginals p(xA) and p(xB) for multivariate Gaussian distribution, where A and B are subsets of x1, x2, ..., xn of jointly Gaussian random variables.

Let’s partition our vector x into two subsets, xA and xB, and then we can write down the mean and covariance matrices in block form:

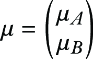
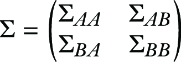
figure
figure

To compute the marginals, we simply read off corresponding rows and columns from mean and covariance:

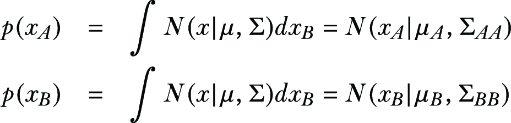
figure

2.3 Let y~ N(μ, Σ), where Σ = LLT. Show that you can get samples y as follows: x ~ N(0, I); y = Lx + μ.

Let y = Lx + μ. Then, E[y]= LE[x]+μ=0+μ=μ. Similarly, cov(y)= L cov(x)LT + 0=LILT=LLT=Σ. Since y is an affine transformation of a Gaussian RV, y is also Gaussian distributed as y~ N(μ, Σ).

3.1 Compute KL divergence between two univariate Guassians: p(x)~ N(μ1,σ12) and q(x)~ N(μ2,σ22).