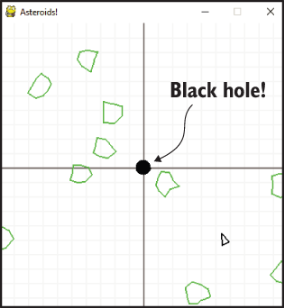
There has just been a catastrophic event in the universe of our asteroid game: a black hole has appeared in the center of the screen! As a result of this new object in our game, shown in figure 11.1, the spaceship and all of the asteroids will feel a “gravitational pull” toward the middle of the screen. This makes the game even more challenging, and it gives us a new mathematical challenge as well−understanding force fields.
Gravity is a familiar example of a force that acts at a distance, meaning that you don’t have to be touching an object to feel its gravitational pull. For instance, when you’re flying on an airplane, you can still walk around normally because, even at 30,000 feet, the Earth is pulling you downward. Magnetism and static electricity are other familiar forces that act at a distance. In physics, we picture sources of these kinds of forces, like magnets or statically charged balloons, as generating an invisible force field around themselves. Anywhere in the Earth’s gravitational force field, called its gravitational field, an object will feel a pull toward the Earth.