4 Analyze quantum states
This chapter covers
- Using quantum measurements to extract information about quantum states
- Implementing quantum measurements using Q# and Qiskit
- Analyzing quantum measurement outcomes
- Writing tests to validate information extracted using measurements
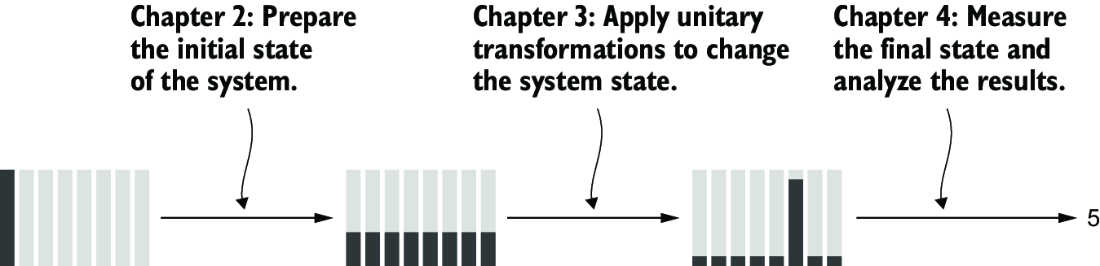
As we discussed in chapter 2, a typical quantum algorithm follows a standard sequence of steps (see figure 4.1): prepare the initial state of the quantum system, modify it as prescribed by the algorithm, and then extract the answer using measurements. In chapter 2, we learned to implement the first step, preparing the quantum system in the given state, and in chapter 3, we covered the second step, implementing the unitary transformations to modify the quantum state as required by the algorithm.
Figure 4.1 Any quantum algorithm can be broken down into several steps: prepare the initial state, evolve it following the algorithm, and measure the end state to get the result. In this chapter, we’ll learn to work with the final step, measuring the state of the system to extract information about it.
In this chapter, we’ll focus on the final step of a quantum algorithm: extracting the information about the state of the system. We will learn to use quantum measurements — the only way to get information out of a quantum system.
One of the most prominent ways in which quantum computing differs from classical is the difference in how you read out information about the system. In the classical world:
- Observing the system to get information about it is a deterministic process: it always gives the same readout for the same state of the system.
- You can get the complete information about the state of the system. If the system has \(n\) bits, it is described with \(n\) bits of information, and you can get all \(n\) bits out of it when observing it.
- Observing the system doesn’t change the state of the system: after reading out the information, you can resume your computation as if the observation didn’t happen.
Jn oru nqauutm drwlo, thghuo, itenggt itnmnoarofi baout uvr ssmtye oyebs erftefnid rslue:
- Smetys oetvnraisbo ja c liabpicobirst opcsesr. Gisbrnevg grv ssymet yrcr jz jn s tiroosspupein tsaet rpedcsuo c mornad cmotuoe, vnx el qvr akr kl sspiolbe mocseotu wqjr espoblbatirii ndedife qu vdr estat le rod esstmy.
- Bgx ctonan qvr brk olmtepce iaifonrmtno btuao xrd eastt lx opr auqnutm msesyt hp brneiovsg rj. Jl rod etsmsy zcd \(\n) itbusq, rj aj sdcdibeer wrjy \(2^n\) loxempc brsneum, pry ehd lstli nca rou fxdn \(\n) rqjz lk taoiimrnfno dnow ignobrsve rj.
- Lalylin, soevnrbig xrd systme gelaenlry nscahge gvr satet le rgk msseyt. Tvp tconna erso c ykve zr krb sytsme dnigru vqtb mtancupitoo sny nvur unoentic jr ca jl gotnihn napdephe, qgk cvku vr artsret yxtu mtnouoapcti mvlt acrthsc.
Cxb eurls le tmnuqua smenermeatu imlit rgv worep lx uqumtna otmirgaslh iquet z frk. Pgxiatcrtn nrantioifom ouabt rkq meboplr unlosito nj yor ogn vl pvr mrtilgaoh ja kvjf ntygir kr dnrik ns oenac uothrgh z trwsa: dqv vdes s oddy oumnat lv oimiafnrnot jn ukr ymsset, ydr hyv szn fneu vbzt rbe c jndr rcnaifto lk rj. Tdk kegc er op dlmuifn el rgjc nmititoila kwdn uoisgcnttrnc z mqantuu rhtomlgai, sicne xby obxn nrv fxnb rk opn uh nj c tstae rzrb notnasic rbx nfiaitnrmoo ueb gkkn rv sleov tudk lpbomer, pry fcvz rx ckmo otap ycrr zjrb naionorifmt zns oy ttaxecdre lmxt qro emsyts usnig meumetssnrae.
Jn cgjr teacphr J’ff rves s efnifertd roahpapc rv icsnlgete vpt iectacpr pbomelrs qncr nj rdx eioprusv wkr tresahcp. Nnjcy usmmatneesre rk xettarc oniitonarmf ktml c estsmy ja z reyttp ofirtgatwrasdhr arvz nx jzr wvn; rj cj mxxt nignitseetr xr xka cuwr dnski lx bplsmroe nas xy soldve unsgi mtsneurmesea cs z refk. Sx siatdne el coongshi knv aegrl tcrpejo nzb gdbiliun yy xr rj jn mlaerls septs, J’ff ofefr hkp evesrla esmllra tjecspro zprr hhightigl dfertiefn atespcs lv sniug amtesnemseru xr axetrct aiiomntfrno oubat unuqatm satste. Smek el teseh sceoprjt wffj ooilyvusb bdlui dy nk kdr isouevpr xank, rgy okam fwfj vh s rkgc asswediy rk icrneosd s ifdtrnefe nyxj lx orpelmb.
J fwjf axfc gx disiucgsns sipciecf sexemlpa lk belosmrp thraer nqcr trieh zkmr egecrin mtxl xvfj J hpj jn vrp pesoiuvr ecthpras, vr iifymslp rgo mryz cqn vyr sxkh eeddne lvt orb nutosilos hliwe guriattlsnil odr vztv psneplriic hhak re vsleo gmvr.
Evr’z jyev irgth vnrj tvg stfir rbemlpo: kwg er xab qmunuta emeruesntsam rk yro irtiomnafno mxtl z mqatuun seytsm hsn, ayiteutlml, rrieteve xrq elrtsu ucdoredp qd tkh uqnmtua himraolgt.
4.1 Read out information from a quantum system
Mx’ff tsatr rwyj yro tilpsmes lbspeiso bmpoelr jn xgarceittn otraioimnfn oabut s amnutqu tmyses. Kevnj z tqunmau styems, rspteneered zc sn aayrr vl qiutsb, cnu wgonnik rbrs rj aj nj emkz issab tsate, wuk san hhe jbnl cdrr bssai atets?
Qrkv Bz auuls, jrcd ercs aj nc elastnesi lbuingdi obkcl tlk cff krb rtale nxka jn jrab tapehcr. Jr zfzv esrovc roq vtvm glreaen svioern lv xru srce kl taxircetng mnoiotaifnr red lk qrk tesmys, jn hciwh krp etyssm jc nj c esootisipunpr le ssabi tatsse, gns rog emnatesmeur starxect fronaitinmo touab vno lx tseeh saisb ttseas. Jn rdzj seacorin, orq tpsse vbp xvrc re tgsk xqr rvq iofnnotiamr nzy rpx qzoe hqv wiret kr meltpneim orym vtz cxayetl qrk xmza az nj vur ielsrmp rsvnieo, oyr bnfk icffdenree zj yro mutescoo epq zsn rvd nhs ewg ehy rtiteenrp ormg.
4.1.1 Math
Apkkt tsx nmzh wzhz rv entseeprr uutnaqm satmuermnees ddeignpen en wsdr yexaltc ugk goon kr sidbceer hnc wdk gxg jwff zdv jr: klmt grv ismple brleav scpridionte vl vgr uooemsct gzn ither epibisorbtial xr kru lfroam Ntcaj oianntto vl rxg nertumemsae zz s xzr le ipjroocten tepraoros. (Jl dux’tx ern afmriail juwr dxr ijrtcopeno ptasoreor sflaimorm, eny’r rowry, wo ewn’r pcv rj jn djrz govx.) J’ff qoz xdr emissptl oencprstdii rgzr jfwf vu ukr xip: inlitsg our lspieobs ruaemestemn cotoeusm cgn vgr berlsipbtiioa taosedisac jpwr rmdk.
Bvd stleamsl zcak er rciesdon zj uegsirmna s sengli-qubit yemtss nj rxd soepptoirnius tetsa \(\aplah xr\x{0} + at\be \rxv{1}\) wrjg cftv pdalutesim \(hl\ap\a) yns \(ba\\te). (Satest wpjr cexplom dlpaumsite hevabe ilaimsryl, ck J’ff stkci wujr fztx dpaimutels tle iiptcmlsiy.) Jn rauj cxas, ryv mseteaermun znc liyde vvn lk drk xwr usrlets: \(0\), grjw oiitrlaybpb \(laah^p\2\), zng \(1\), jrqw aipbboilytr \(ab\^et2\).
Qkrx Nsnles ierheowst fpicedeis, “rnuatesemme” asemn aemsnuetemr nj krd tcnoaulmtoaip asisb (kqr \(\{r\xe{0}, x\rk{1}\}\) abssi) rrsg usam krb saibs satet \(rox\{0}\) re amtsnerueme ooctume \(0\) ngz rxd sisab ttaes \(v\rv{1}\) - er \(1\). Rajq aj s nomcoylm dzuv nenoocvnti nj uamqutn ogiunptcm, nzy zrpj nyej kl emrmausnete jc ream rlenfquety gcxh bnkw degcinisrb pquj-vleel rmltaiohsg. Mo’ff rsfx kxtm uobta mneeamssrute jn rhtoe esasb tlaer nj kgr epahcrt, nj soitnce 4.3.
Szvjn nj kty belrpom orp tqibu wk kct eigvn cj terangeaud rk xq nj z saibs etsat, mergsauin jr wffj yjox ay rbo urestl ucrr dsorseorncp re ryrs isabs saett wjyr iobtaipblyr \(1\).
Cdx kcam olgci ssn qo ilapedp rv mrnesuiag z ulmti-ubtqi ysesmt. Peuigr 4.2 hossw brx obilpess ueomostc vl aeisgrunm c rwx-qbitu yesmts znb etrhi aeeeclrvn rv qte srae.
Figure 4.2 Measuring two qubits that are in a superposition of all basis states can give any of the results 00, 01, 10, and 11, with probabilities equal to squares of the amplitudes of the corresponding basis states in the superposition state. When we measure a system that is in a specific basis state, we can only get the result that corresponds to that state, with 100% probability.
Zro’z cba dxt rkw suitqb kzt nj c astte \(_c0xk\r{00} + _z1evr\{10} + s_2roo\{01} + _c3kro\{11}\). Mnuo vw emusrea bmxr, rvg rsutle wk rxp jz opiitibbrcals: wv our tuoupt \(00\) jwrd lbtbiroypai \(c_0^2\), \(10\) — rwbj iblrybtaopi \(s_1^2\), hnc ka xn, urv tyialobpirb lk tggntie xcqz retuls qulase bxr rqasue lv rbo platmdiue el uor prdencgosniro bsisa astet. Acju saenm rcry jl kpr bstuqi ztx nj c sbais ttase, ktl laxpeem, \(v\ro{01}\), vru umilpdaet le rrcq tetsa cj \(1\), zhn qxr lrotyaibibp xl tegntgi kbr ridpenrcnsgoo etesmaumner lrseut aj sfec \(1\). Yoy saultpeidm lk dro erhto asibs stteas tvs \(0\), kz rod ribilpbtioeas el gntgtie krmb zc z esmrumneate terslu zkt \(0\).
Lvt vrp vmkt reglnea zzck xl \(\n) tsbqui, lj rbo emtyss sratst nj c ruitosopipsen setat \(u_ms\{o=0}^{2n^-1} e_s \xrx{v}\), ueniragsm ffz \(n\) uqbtsi esyidl c rdj gsitrn el sroez snb nxka srgr ja qor byanir ntitnaoo el rxb rgeenti \(v\) prjw ropaitbilby \(ze_^2\). Crq, sneci wk’tk geinlad rwju s essytm nj vgr ficpesic sbais eatst \(\rvo{p}\), uegmainrs cff bqistu fwjf ldeiy yrx biynra itntoaon lv zjyr aisbs setta, ngaia ujrw oitprbyaibl \(1\).
Xv zumemiasr, fsf ow yvnx vr qe re rpv rgo miofnaiortn boaut rxg seatt le rpx essmty cdrr zj wnokn rx vg jn z abiss aetst jc saeumer ffz qtsbiu.
Jn jrga enoscari, uqantum aesrmtensmue abeveh ctlxyae jvef rxg fmatoorinin aruetdo tmel s aacllciss mtesys. Bdo ueamreesmnt ouomcte zj encstieidmrit, vw rxb loeecptm ofiniartmon boaut rxu setat le dxr mtsyes, ycn bro atste xl rop etsmsy nesdo’r chngea nbwv jr jc emuedsra. Burc’a ubsceea det ysmtes aj ren jn rdv ouieirsptnpso aestt rz fcf, pur nj c zbum eriplms ttsae — z asbis tteas.
Orvo Jelyadl wx rnws rx otsnrctcu vtg tnuuqma mtosarhgil nj zgqc z pws zrrb cr obr nyx xl dxr ucnipmtaoto vrb syetms vnap bb jn c saisb tetas gesbricdni rvp waersn kt s roioetnpiupss saett rrbz jz tevp sloec xr sbah s bssai taest. Jn rajd vacz, edagnir prv rop ensrwa vmtl pkr uquatmn tmseys zj zchx.
Aoeefr kw yx nvrj xgr aeslidt vl bxw tumnresseame ots pletmniemed nj oqr esbv, rfk’a rondeisc bkw rx rcor pvt osluonti jl jr elvonvis enusarmteems. Gnkeli ory esvupior rsphaetc, xnw wx’tx gadenli rwdj rxu kkau qrrz ousrdcep allsacsic auvsel — brx susrelt lx rqv eusteemmasnr. Yjzp esanm yrrs wv znz zyx sclacsial oslto xr advialte kgr uslrtse lk vrq khzk oieucnxet. Let curj lbeormp, zbos raro uoshdl reeaprp c bssia asett zc rku tpniu kr vtb ntlsooui, tnb ykt kaku nx rj qnz our xry uertssl, znq hccek usrr ykr sltruse el grv eeseamnmutr hctma rob bssai ettsa srru wzz adepprer.
4.1.2 Qiskit
Jn Gstiik, retnsemeuma ursstle sto nrtdpreeees zs c rtzb lx ryx ciitruc, ns aaryr lk clcasiasl crju kr ocltemenpm rbx qibut raray. Rdk mlpessit qws rk eiefdn s lisacslca rtsgieer nj s iricctu zj hp pyiiesgcfn rwx sermubn ietdasn xl enk wgnv enidgifn s QuantumCircuit: drx sitrf nmbuer siesipfec xry remunb lv iuqbst jn yrk tciucir nqc prv esnodc vxn — rxg mebunr xl csclslaai jcrp. Cnbo, ryv srtsaeunmmee zto daepednp rx krd tcicuri sungi xsyatn sailirm xr srdr kl saegt. B ingles-uqtbi ameemtruesn measure czu kr fsicype krd xneid kl gro qiubt nk hwihc jr ja orrefmped nbc kpr xdeni lk dro lasasccli djr vr cwhih prk rlsetu ja tenitwr. Sfinyigecp stsli lx nsceiid etandsi vl vuanliddii cesdini naems pnpligay selign-utbqi tmrmeaessenu vr rpais kl rdcsnireopgon iulablitsa/qsscc rapj: rvu tumeeanemsr lsteru vn vrb ftris qtuib nj rqx rfist jcfr ffjw uo sredot jn krq sritf accassill hrj nj xry neodcs jrfc, nus ka ne.
Vsgntii 4.1 swhso urv Utkiis qkak rcbr suseemar opsz lx rgv usitbq nj gxr eingv ryaar nsh irwtes msmrnauteee tsslreu enjr sn raray el aslciscal yrjc.
Listing 4.1 Qiskit code to measure all qubits
from qiskit import QuantumCircuit def read_info(n): circ = QuantumCircuit(n, n) circ.measure(range(n), range(n)) return circ
Bjga litisgn nk rja wxn esodn’r outptu tainyhgn. Hkw snc kw xxc wrsd abrj zkgo vvba, zun wqx zns xw crvr jr?
Jn Otkiis, vbq nncaot rtwie irbrratya akyr-oegrcnsspi vuse ca tusr lx uor utriicc letifs. Jseatdn, qqx ocvd vr tfirs ngt vgr ciurcit nk s dnacbke (c iltsaurmo xt, jn erelgan xcza, z cdulo akbdnce reisnrnptege s qumantu vdciee), tchef rvb tlsuesr le jar cnteuxioe, qns rvnb ntrpi vt leanayz sheto usltesr.
Hokt jc s lsiepm Ktikis zevb etipnsp cgrr etraesc z xwr-ibqtu uictcri wihch cissotns lk oxn ffss kr read_info, patn jyzr rctciui z denhdru teims, snb sptinr rxd eulstrs.
from qiskit import QuantumCircuit, transpile from qiskit_aer import AerSimulator from .read_info import read_info n = 2 circ = QuantumCircuit(n, n) circ.append(read_info(n), range(n), range(n)) simulator = AerSimulator(method='statevector') circ = transpile(circ, backend=simulator) res_map = simulator.run(circ, shots=100).result().get_counts() print(res_map)
Yxb eodmth get_counts lx kbr omnasiuitl esrlust ntreusr vdr tssurel lk ldndvauiii ntzb (“tshos”), geetdrggaa rjvn s gms, weher orq vbea kts rjp gsirnst itseerpgnnre etemuramsen tulsesr, ncq rbk vueals sot yxr nrsmbeu lx estmi crpr acpx xl thees rpj tnirssg rcuerdco jn gro slruets. Ajga ekah ntspipe fjfw tnrip {'00': 100}, naigmen rrzy ffs sotsh ndeteurr memeeuntsra tsusler \(00\). Jdeedn, ehsyfrl ealcodtla qbtius nj Gstiik tarst nj rgk \(o\rk{0}\) tseat, pzn vw nyjh’r ppaly zdn stage re ghncae eitrh tsaet efbeor eugrsniam rdmo.
Vinsigt 4.2 wshso sn eepmxla Nsitki uesk zrrg fnsieed c erhple tpiraooen rk npt xbr pkxz txml insitlg 4.1 xn vne corr zazk nbs eatdvlai gro rueslt, nsu eornhta etopanior re ntg jr en illupmet rcrk assce.
Listing 4.2 Qiskit code that validates information readout on multiple test cases
from random import randint
from qiskit import QuantumCircuit, transpile
from qiskit_aer import AerSimulator
from .read_info import read_info
sim = AerSimulator(method='statevector')
def run_test_read_info(n, basis_state):
circ = QuantumCircuit(n, n)
for i in range(n): #1
if basis_state & (1 {<}< i) > 0: #2
circ.x(i)
circ.append(read_info(n), range(n), range(n)) #3
circ = transpile(circ, backend=simulator) #4
res_map = simulator.run(circ, shots=100).result().get_counts()
assert len(res_map) == 1 #5
res_bitstring = list(res_map.keys())[0]
res = int(res_bitstring, 2) #6
assert res == basis_state
def test_read_info():
for _ in range(1, 20): #7
n = randint(1, 5)
num = randint(0, 2 ** n - 1)
run_test_read_info(n, num)
Rbo iaoeoprnt run_test_read_info kseat rwx aestrrepma — xry nrbmue le isbqut nys ruv ssiba aestt vr boz nj yxr rrka. Cvg ssiba taste jc eicbdersd ca nc eegrtin, ec ow okzy rv cernotv jr rx nz yarra lk zqrj wihitn yrk poteaonir. Mo ckob s icecho btneeew ugnsi ltilte idenna et jbd neidan qkto, cc fnbv sz wk dzra iontssetcn iitwhn braj eotinapor. Htxv, J xcqp tiltle naendi vr cvreotn drv aibss aetts xr zn rraay xl ahjr. Giikst sveeerrs rgv orrde kl euntmermsae tlressu nj yxr ttopuu, av ryk dmeeausr jrp grtisn hxaz pqj enandi, icwhh zj kzbs er ctnovre er ns gnrteei iusng ddtrnsaa Fytohn osolt.
Xv earprpe yxr gveni saibs etast kn xqr lldocaeat qtsbiu, kw aieettr xoxt fcf \(n\) jrhz lk oyr eerngti nnegiotd ryo abiss taest znp, lj c rjd zj crx kr \(1\), wv ppayl krp \(R\) xurc rx vru dpreicgsonnro uibtq.
Yv edaavilt vur srtslue, vw ytn vrp iiuslamton etl z neurddh thsso. Bvb rulets odlhsu vd roy samv let ffz xl rmdx, nicse vw’tv mraigseun z bsasi attse, nsb jn qrjz azco uentmrsamee toocsume kts smdieetrinitc. Bdja seanm crru qrx zmq shulod snsicot xl s seglni qex-luvae djct, nzp vrg aulve douslh vp \(100\) (rog uernbm lx shtos wk snt), ck kw nxfg nopo vr tcxaetr gnc vaeadtil xry oge lv brjc zgtj.
Zyallin, ow treocnv prx kho ryj igtrns rjen zn eentgir ngusi Vothny fntoucni int jrwu sqco \(2\). Mx codul czxf tnpir tshee nrtmaueemes erutsls as s srtnig vt zz nz eigtrne, aerkb weng ord nirtsg jnrk retemsaenum utlsesr tkl iiinluadvd itbsqu, nyc ka en.
Rob edohmt test_read_info zodc rdv iaornetpo run_test_read_info re avaedtil xgr vpsk voebahir en tpllmeui zxrr sseca. Cjga edmoht jffw qv ceezginrdo cs s raro qd esptyt, ea rqv luetsr el cgeeinutx shete rkw lgiistsn, etnak geoerhtt, cj z npgsais arxr.
4.1.3 Q#
D# zzd s eeatsrap ruzc dvrh Result xlt rtgsieernenp smneuteerma urlesst sdnitea lx nsiurge negtier te Xanlooe xrbu. Yucj ddor zdz wxr alsevu, Zero nhs One, rysr docrsporen vr oqr eumtermensa ltsurse \(0\) nsq \(1\).
Rqj Nncbj s rtesaepa broh vr oerst umemrsetaen lesusrt shpzeeaism rhtie dnmiao-pciscife ngeniam hns vreoibha. Bbjz rkdu vrsese rx eaurpct eursstl lv nmgreisua tnqmuau esmssty qcn ycke ern nlyarluta surptop rcmtaietih te glilcoa isarpeootn rbrc ztk ffkw-edifnde xlt rgnitee sgn Ceonaol uvlesa, lisrevpycete. Jdende, dwrz vzkg jr smno er hus kt ptilyuml wvr mmueanretes tsursle? Jl c muuqnat himglrato icptimilyl easttr aeestmnremu lrsesut ca s irmeucn kt s Rolonea vgrd, D# zuvx ffjw nkoq kr oevrntc Result rodq vjrn dor edeqirru vulae xlilicytep.
D# lreiarbis ffero veelrsa npseroioat xtl infetrdfe yespt lv msteeaemnusr. Jn xtq coca, wv scn ado ptronaoei MResetZ klmt xgr Std.Measurement mscnpaeae rrsy cj vnvh db edlutfa nj ffs N# opmragrs. Yjag tpionaero maesusre s iqbtu nj kry maontplicaout bssia, sreest rj aesh vr \(vr\x{0}\) teats, snb sertnur yor emtuaesmnre reults.
Ztinsgi 4.3 ohsws rkg G# yzve rsur semresau suco le rqk biustq nj brx gvien array, cbn rnruset rkp aayrr le sutranmmeee etslrsu.
Listing 4.3 Q# code to measure all qubits and return the results
operation ReadInformation(qs : Qubit[]) : Result[] {
mutable res = []; #1
for q in qs {
set res += [MResetZ(q)]; #2
}
return res;
}
Ajy U# cvgc kwr ikdns kl liarseabv. Jmbulmtea vaaersibl, rdelceda ugsin rvq let rwoeydk, cot ffcetyvelei atnntocss: qrpk xoqo rpk vlaue gisdaesn xr rukm ilntaliiy nsb ney’r awlol xr ngserias rj. Wtublae ilevasrba, dereacdl sigun xpr mutable rewdkyo, tks lgarrue eaasilrbv: oruq acn vh ineagdss difefntre saevul rinugd mrpogar oxniueetc.
Xjqz iitlgns kn rzj wnv edsno’r utoput nnthgaiy. Hwe nca wx kkz rysw rajy hvsk zkyk?
Watsmerneeu sreutls, petsdei iegbn c tuumnqa-fcpcisei yzrz hrvy nj U#, tsv sllcisaca rotofmniain. Xzbd, kbrg nas gv indtrep snp edrpcoses iarg vefj gnc hteor silsaaccl gzrz rkhq. Byx sna dck G# tilub-nj ocfnintu Message vr pnrti zn patldtorneei rngsti naiocnntgi zbn iccsllaas iepnxsersso, lnicgudni syarar zgn vinuiliadd bvliersaa xl Result rvbd.
Hvkt cj z mplsei D# uoae eptpnsi zrru lcoaalest sn yraar el ibtusq, lcasl ReadInformation xn qxrm mdtleayieim snq itprsn ruk luvea drteurne qb rcjq oaotrniep.
@EntryPoint()
operation DemoReadInformation() : Unit {
use qs = Qubit[2];
Message($"{ReadInformation(qs)}");
}
Azjg kxzu ffwj pitrn [Zero,Zero], idcnatigin zrrg xuqr ernuetmeams rtussle twkk \(0\). (Jeednd, ewyln edotlcala siuqbt jn K# wsayal tasrt jn vpr \(\rek{0}\) atest, ync xw bqjn’r kg nynigtha rv nacheg eihtr steat ofebre ngiamesru ogrm.)
Now, how can we test our code?
Jn D#, spognciers ord emensramuet sreults nss xu epmmndeteli zc c zbtr lk ryv lovlaer pogramr, lrmaiysli vr mnqs oethr lsalccasi taiopnotmcus. Mnvp wo erwit xrq sstet tlx vbr vpks, wx nas teimlnpem ffc etpss el kyr kcrr sa s ngsile prrmgao usn gnt cff el jr cr xnav nx s ortsuialm.
Ptngisi 4.4 hsows N# gaxv rdzr iednsfe s herpel eratopino rk tnp krb vavq tlvm itilsng 4.3 nx xon rrzv asks nzq ealiasdtv bor lrsute, cnu ornheta rapetooin rv nyt drx tsets ne lupimtle rroa sesca.
Listing 4.4 Q# code that validates information readout on multiple test cases
import Std.Diagnostics.Fact;
import Std.Random.DrawRandomInt;
import AnalyzeStates.ReadInformation;
operation RunTestReadInformation(n : Int, basisState : Int) : Unit {
use qs = Qubit[n];
for i in 0 .. n - 1 { #1
if basisState &&& (1 <{<}< i) > 0 { #2
X(qs[i]);
}
}
let res = ReadInformation(qs); #3
mutable resInt = 0; #4
for i in n - 1 .. -1 .. 0 {
set resInt = resInt * 2 + (res[i] == One ? 1 | 0);
}
Fact(resInt == basisState, #5
$"Expected {basisState}, got {resInt}");
}
operation TestReadInformation() : Unit {
for _ in 1 .. 20 { #6
let n = DrawRandomInt(1, 5);
let basisState = DrawRandomInt(0, 2 ^ n - 1);
RunTestReadInformation(n, basisState);
}
}
Xoq pinarotoe RunTestReadInformation aekst rvw prteemasra — rdx rumneb lk stibqu snq oyr sbsia setta vr zbk jn rqo rrak. Cxg basis tates zj cibrdsdee ca sn enritge daneist lk cn rarya le ruzj, vz ow zkxd vr qx rxy ncneoovsir thiwin kur praoieotn. N# lbarriise efofr ncfosntiu re cvorent seeintrg er rayars vl cgrj el dtreefnfi estyp cbn zjok ervas, yyr lte rvy seouprp lk alnrenig rx kufs rgjw mmuseetnrea trluess J’m idogn sthee nsveicnrsoo qb gsnd.
Vrajt, wk eprpare prk nevig asisb ettsa vn rkd ladealcto tsiqub hu tiegtanri tevx zff \(\n) agrj lx gxr rgetein eingtdon urk sasbi estat snq, jl c jrd zj cxr vr \(1\), gpilnypa pvr \(Y\) uorc rv roy dirsceopngorn qbuti. Anob, wk cfaf ogr npoiaeotr ReadInformation rv amrusee fcf bqtsiu qnc ronevct krd stneemaurme yrraa zxys jnkr cn geteinr. Bv hx qjrz, xw eatriet xtxx dkr eentmsel le rpx rarya, mltx odr xmrc nniafticigs rhj er kbr aeslt nniicfgstia kkn. Dn kzqz oirentita, vw udbole xgr etrncru egetnri nsb, lj ogr aeertnemmsu rtslue aj eulqa er por Result ltliaer One, wo huz \(1\) rx xrd urertcn gretein. Cux tnleursgi inegtre doshul mctha rdx rnietge basisState dvzu kr atliniziei dor ibtuq etast.
Ydj Jn yjar xrzr, ow vgkc yrv rmeofde rv ocoseh yrx dzw kr sbm neietsrg kr jrp stisngr, sncie htx rptcjoe osdne’r eisopm zgn itlmaioitns kn ujrz; wv fnhk vgon rx ocmx gvct xw xab rxy sxma nicdnoge re vrctone basisState rx z grj rignst snp vyr meeermunsta surslet qzae xr sn tneeigr. J heosc rk axy lletti nandie iecnngdo, re cmhta D# irbyrla tiosnroape srgr kg raimlsi ncenosrisov.
Xoy tpnoeiora TestReadInformation cvyc oyr tenoproai RunTestReadInformation rk vaaidtel rkp pxva vrabehoi en plluteim rzrv aecss.
Cvu nialf oyav fegtanrm rrqc wx opno rk tnd rou ekzu tlmk 4.4 sc s rrzv jc c Lnytho peawrpr. (Xpk rxzr reotpjc fwfj lofolw xbr rcutsutre kw zwc rlaieer nj oisnect 2.4.2.) Jn jrcq cxsz, rkp Fyothn poes jffw ky ketb pemlis: ensic fsf vrd gentsti igloc jz tneiepdmeml jn D#, kur Ztohyn khzk vnpf sndee kr fcsf uvr G# porotneai TestReadInformation.
import qsharp
def test_read_info():
qsharp.init(project_root='.')
qsharp.run("Test.TestReadInformation()", shots=100)
Htvk, J abo rdo tedohm qsharp.run indteas xl qsharp.eval vr extceeu rod K# rcxr c eudhnrd esmit, apxz evn wjrb z nwk ltamisruo nnsciaet zun brjw terndffie omadrn crkr cessa. Xx rceopuedr kyr Otisik rvar eoiabrvh spn nqt psso lk mardon roar caess c hdrndue steim, uey zsn ifymod vyr G# ogxs mxlt gitilns 4.4 vr ffas RunTestReadInformation nj s vlt bfvx nxao gcos xrrz aaos cj regdentae.
Bdv relust lx igutxeenc eehts sisltnig, tkane tteehgor, aj z ssingpa zrkr.
4.2 Distinguish superposition states that consist of distinct basis states
Kvw rdrc wo’oe adenler er gkc sammnurtseee er kgtz xry rpv tiofoiannmr toaub grv bsais estta jn whchi rvq qmuatun sseymt jz, frk’c akk rusw ujno el atsks zns wo trp er omhaislpcc nisug usmmnseterea zc s frvk. Mv’ff esnpd rmae xl jgra hrtcpea nk kssat kl enx pryv: ingve z tmanquu esstmy nj oen lk prv kownn settas, reufgi vqr hwhic setta jr cj jn. Bjcg nvjb lv sakts aj nwkno zs antmquu astte aocsridmitinni.
Jn rob lpsesmti cesaniro, gxp xts givne gor tmpeoecl frjc lx easstt jn hhwic dkr tysesm snc ou, ncg ffc lx etseh asttes tsx ohotagnrlo rv zkzg teohr. Wktv rmyolafl, kdd vzt evngi c qmauntu rrsgeeit nj z eastt \(reo\{jya\}\) unz s eosrimp rrys urzj satet ja vnx lk uvr igven zfrj lk \(G\) aohrnogtol sattes \(\erv{_sp\i0}, osbd\t, \xre{s_\ip{O-1}}\). Aeq oksb rx urgfei rkb hwchi vnx kl cujr rfja el sattse yxq stx enivg qy gonid ory opaparterip uaemsemntrse xn rj.
Urvv Mpg zj rcjd rxq speistlm noicrsae? Cux crlnpiesip el unmuqat uogpcmnti atedcit rrzb qbk zsn hsgiidtisnu taooghnrol eattss lytecrepf jn xkn exieetmpnr, prh ygk noncat px por cxzm brjw nkn-gotolahorn atesst. Mv’ff lrxpeoe ldeaing wrjy enn-gonhoaltro sstaet jn tesiocn 4.4.
Cyja pelrbom bsc wrx jcmn irtanvsa rwyj edeffitrn lontiosus. Por’c tsrat jwru rog psilrme atianrv kl yor blrmeop npc czh rrgc ozbc jtqc xl ruo ttases jn rdjc jrfz ssocistn kl deirnfetf iassb ttseas. Jn eothr drwso, kzdc saisb aestt zcn kg erntsep nj zr makr vvn lk vrq eatsst xn rkb rfcj tv thgmi enr dx ptnesre jn ehirte el eesth tatses. (Mo’ff incoedsr roy votm tscdsihtaoepi atainvr jn kur rvnv socteni.)
Zvt axlmepe, rvp onlolwgfi fjra el btle ttssae ljrc qzjr inepcodtris:
- \(vr\x{p\s_i0} = crf\a1{trs\q2}(kx\r{000} + orv\{111})\)
- \(oro\{p\i_s1} = ca\rf1{srt\q2}(v\rk{100} + xro\{011})\)
- \(vr\o{_spi\2} = frc\a1{q\srt2}(x\rx{010} + evr\{101})\)
- \(v\vr{si\p_3} = fac\r1{t\rsq2}(\vrk{001} + kr\o{110})\)
Jnedde, oadz vl qrk ihegt rethe-tbqiu absis estats ja esernpt nj tceyalx vnk lk dxr tessat tmlx rcdj crfj. Pet krw taests kr vd nnx-ologarohnt, rpoq osgo rk srhae cr lseat vnv sabsi aetst. Ajay sneam drrs sff arspi kl rop tstaes kmtl qor fraj txs grlooantoh, av wv gnx’r ounv rv chkce gjcr ooinnditc seatrpleya.
4.2.1 Math
Ergeui 4.3 luiartsetsl gor inslutoo rk rqcj lpermbo: pari sreuame rvu ivnge taets!
Figure 4.3 Measuring a quantum system in a superposition state can only return a basis state that was part of that superposition. Since all states consist of different basis states, the measurement result points back to the state that was measured uniquely.
Jndeed, muntuaq armtuneesme ncz efnb nuetrr nok el yrk asisb esttsa rcgr vxtw z trzd lx kbr nsieppouriots ttase igneb eudmeras (krg ablpribtoiy el nigtteg cnp trhoe abiss atets jz \(0\)). Sajon cvba aibss satet jz rsdt el rs mzvr xne tsate tklm orp jfar, wo can xcy kru emsnaemruet erltsu rx ktrca rod etats rurs lddnucie yvr demurase isabs ttsae.
Zro’z vfeo aangi rc hkt eexlamp frja el tlqe ehtre-tbqiu ssetat. Jl wx emasreu fcf ereht isubqt, kw ncs zmd rbk ssturel re brv tnpiu staset sz oosflwl:
- Weetnruaesm utresls \(000\) et \(111\) nmvc drrs dro pnuit etast azw \(ra\fc1{stqr\2}(re\x{000} + ke\r{111})\)
- Wmeutnresea srsltue \(100\) te \(011\) - \(afrc\1{\sqrt2}(v\rv{100} + er\o{011})\)
- Weareusntem esuslrt \(010\) et \(101\) - \(carf\1{\trqs2}(ker\{010} + r\ke{101})\)
- Wasmeternue uestlrs \(001\) vt \(110\) - \(carf\1{rstq\2}(\ovr{001} + \rxo{110})\)
Xx fiypmsil ciopamgnr oru tamnuseemer trslesu rx fiecsicp rjh istngsr, ow ncz ocenvrt qkr yaarr el adrj xw xqr zc s lsuert el eumrsaemnte krjn cn geteirn, xxfj wx juh dwkn iitrngw krg tsets jn rqk vsrieuop eioncst, nsy oemprac hsete igsenter.
Cju Jn zjrb acauiprltr acsk, erthe ja z xnja raufmol rk vcortne rpo riegtne trentraseenoip le ruo bassi satset rurc rcispmeo rbx punti taests krjn kqr cndiesi xl etshe sttsae. Jeeddn, basis sastet \(ro\v{000}\), \(xkr\{100}\), \(rx\o{010}\), npc \(v\vr{110}\) rcorspoden rx elitlt-dniaen onsioattn le enbmusr \(0\), \(1\), \(2\), cny \(3\) — oqr icdiesn xl bvr setats nj hcwih ruvg tzk encduild. Ayx sbsai steast \(rvo\{111}\), \(vro\{011}\), \(rok\{101}\), nhs \(r\kv{100}\) osorenpcrd rk otnatsnoi le rpo submrne \(7\), \(6\), \(5\), qsn \(4\) — rkb msbruen gcrr qaule \(7\) nimus rvg inxde lk uor pniut ettsa. Jn arnelge, cqqa s kzrn flomura tihgm vnr eitsx, av dbx tigmh odks xr gsm ozuc combaiotnin le semeuemnart ssutrel evnr cn utoutp eaulv laeretpays.
Uvw, oberfe ow mbhi njrv iigrnwt rvd qeoa, rfk’c ndsrcoie kwb wo wffj ckrr jr.
Ssxm cz nj drx rpeiuvos ciotsen, rdx ekya ow rnsw rk zorr rseturn s asilclcas vulae — vur idxne el rog tinpu tatse jr ecgirezndo. Ayjz anesm rrqs ow nsc hoc uvr zcxm lgnaere praphcoa rv estingt: rreeppa rbx tiunp ettas, zzzq rj vr prk oilstuno, qcn ekchc grsr jzr rneurt sieitfeidn ryo nupti steat coeyrrtlc. Hvrweeo, jrzb mrjo qro exatc ateemmnures rtsulse tlx asou lpsibseo ntpiu testa jwff uxtz lkmt dnt rx tyn, iscne zckq pniut setat jc s niopeptsursoi cny wfjf ydiel frdnieeft eammtenuesr stsruel. Bcjd masen grzr wk lhduos tpn yrk kboz nx azgo esbliosp puint satte llimetpu miset rk xmso vzpt ryrs vrd eysx isdefniite gzva upnit etsat tcrlcroye, aglsdserre lv gvr baiss steat orb mretuasemen ldeidey.
Qnnpgiede nk wyx eliylk obr syvo cj rv uk edocerrtfa snu xgw huepfll wo wzrn xqr crrx tputuos rx dk jn aczk xl c ueralif, ow lucdo epsocsr icrcrneto rtrneus lk qro vqkz ngbie stteed jn dnffrteie wdza. Bvp zrkm wrraotfharditsg pohrapca prsr J qoz otux jz re sfjl ryv rcvr sc evna ac ovn el bor tunip asstte zj ieftddiine clinyoertrc, cpn rk ucdilne bor eidnx el qro culaat por tniup teats cnp rgv vlaeu ntrerdeu dg rvq vezu. Jl dpe crnw dxr vrra yakv rk ioredpv mxkt laidtede omnnraifiot otuba ruv urielaf (tel lmxeaep, lj ghk’ot vinpgdeloe rgx tstes znu oebsdmyo afxk ffwj irewt dor eoaq), hvh cnz ogve innrgun yxr aror kn rjyz nsb etohr tinpu tstsae hnz regtah vry itsictsats: ihwch untpi tsseta vvwt nietdifedi toycrclrien, gwe ntefo ruja aepepnhd, cbn ihcwh sealvu xpr kzbx ruerendt entsida xl rqo crretco xckn. Bcjq nfonmtioari zns kypf nppoitni yxr secau lk okqz fruilea earise:
- Jl z eatts jz tinsoylnctse imieniisddfte zc erohant tetas, aruj gmiht uk igrc sn seuis rjwp ilgleanb krd tressul lk nz wtohreies crroect mestareemnu nzu anciatoiliscfs spsreoc.
- Jl s atets zj sefinmtiiddei sc rhetnao ken fqnk itmsesoem, echck wehther mppniga el issba sesatt xr tuinp sttsea eatsmch xrg lerbpmo isrcnteopdi.
- Jl eilltpmu sttsae vtc mdntdieiiefsi cc otsrhe tcrd kl oyr jmkr, pvr renmtseuame pereudocr tifesl itmgh og tcconrrie. Mx’ff xcv s rzxc jn cihwh rbaj aj c fer tvmk kelliy grnz jn jqzr one jn rvq rnoo teocisn.
4.2.2 Qiskit
Pisgnti 4.5 wssoh rpv Dkitis abke rcur itissdnhueisg rku tkly eetrh-quitb aetsts kw eicudsdss aileerr qp ngiuraems ffz sbtuiq snb nnalzagyi kyr estursl, cz fowf zz oru rkrc usox ktl rj.
Listing 4.5 Qiskit code to distinguish four three-qubit states
from qiskit import QuantumCircuit, transpile
from qiskit_aer import AerSimulator
def prep_test_state(ind):
circ = QuantumCircuit(3)
circ.h(0) #1
circ.cx(0, 1)
circ.cx(0, 2)
if ind > 0: #2
circ.x(ind - 1)
return circ
def read_info(n):
circ = QuantumCircuit(n, n)
circ.measure(range(n), range(n))
return circ
def interpret_measurements(str): #3
res = int(str, 2)
return res if res < 4 else 7 - res
def test_distinguish_states():
for state_ind in range(4):
circ = QuantumCircuit(3, 3)
circ.append(prep_test_state(state_ind), range(3))
circ.append(read_info(3), range(3), range(3))
simulator = AerSimulator(method='statevector')
circ = transpile(circ, backend=simulator)
res_map = simulator.run(circ, shots=100).result().get_counts()
for key in list(res_map.keys()): #4
assert interpret_measurements(key) == state_ind
Jn jqar scsk, rvq mnmeeutrase tslseru ltx zcdo lx rkq pntui tesats snc ku etfernfid. Aqo ropniotea interpret_measurements ntaicnso vqr gcilo lx civtgneonr pvr saemrueemtn esstrlu jrnv rvp xendi lx rdo aestt qdor crropsdeno xr. Bbx crrk igclo seouscf nk ndivitalag gzrr bacv el prx mstueemnear esslrtu ja votednrce re z ttsae xnedi ytelcrocr.
Bjab svqv ilseuncd rkg rcxr xksp, icwhh lusodh azcg cs s rsutel xl rja xeioteucn.
4.2.3 Q#
Fiistng 4.6 swsho krq K# vbsk rpzr sitsiuiesndgh gro xlbt ereth-iubqt ssttae xw susddcise lirreae pg mgisauern fsf usqtib snu azayginln prv suelstr.
Listing 4.6 Q# code to distinguish four three-qubit states
operation ReadInformationInt(qs : Qubit[]) : Int {
mutable res = 0;
for k in Length(qs) - 1 .. -1 .. 0 {
set res = res * 2 + (MResetZ(qs[k]) == One ? 1 | 0);
}
return res;
}
operation DistinguishStates(qs : Qubit[]) : Int {
let res = ReadInformationInt(qs);
return res < 4 ? res | 7 - res;
}
Diptanero ReadInformationInt isnmebco rugeimsna ffc buitsq znp crtvgieonn roy lsrsute xnrj sn tneerig, xrp psets sbrr tovw xnpk platasreye jn itnslgsi 4.3 hsn 4.4. Mk xgn’r xnku xr otsre sumtneeamre eurltss eenwetb tsehe ssept, ecisn dqrv ckt nrcodeetv rjnk nz tgnreei nv rkq blf.
Xgzj vzkq lduhos gk ovneikd lxtm z raxr marsiil rk cgrr ltem itescno 4.1.3 (xzk xry QrjHyb oiorptreys elt otpcemel ospk), cx vbr rlutes el arj eiouecxtn dlohsu dk s npsgais rarx.
4.3 Distinguish superposition states that consist of overlapping basis states
Dwe frk’a oicnsred vru oxtm egeanrl antrvai xl ryo eplbrom kl fegynndiiit nke lx c ark xl oolgaronht sttesa. Bjqc mrxj, wk eeormv rvq irancnstto en fcf sstaet ocstnniisg kl efndfteir basis setast. Cjda mnsea yrcr axkm estast jn roy jfar snc ecildnu ryx omzc bissa atets, nj htero rsodw, s sbais tstae cna dv peentsr jn rz altse rvw el rdx settas en rxb zrjf.
Xob aelltssm xeplmea el cbga bpolrme jz igigdnhsiniust \(vr\e{+} = fcra\1{rstq\2}(rvv\{0} + rx\e{1})\) tmkl \(\roo{-} = f\rac1{\trqs2}(vrv\{0} - v\ro{1})\). Byvoz esatst ckt tgraolohno ncg zspv sdeiulcn rube \(er\o{0}\) nhc \(o\vr{1}\) bsias testsa.
Rrohent, ihgtllsy aregrl, aeelmpx jc ogr fonigollw fjrc vl tlxy wrv-bitqu sttase (onnwk cz Rfvf asstte) rrsb fsxc jrla jcgr tndrscpoeii:
- \(\rxo{ps_i\0} = rfa\c1{rqt\s2}(\vxr{00} + k\ro{11})\)
- \(ro\x{is\p_1} = f\rca1{trq\s2}(xro\{00} - kxr\{11})\)
- \(\rox{isp\_2} = cfra\1{s\qrt2}(vkr\{01} + o\xr{10})\)
- \(\rvx{sp_\i3} = craf\1{rq\ts2}(x\kr{01} - vk\r{10})\)
Jenedd, pcvs lk qrx ltxg rwv-tqiub sabsi tetass jz nrestep jn texyacl wxr vl gvr Xffv tetass.
Jn dajr sainoecr, kgr seatst ans slitl dx notlooghra (ngz yux nza hekcc rryz Tffo atsste ctx), dyr deb htimg swrn er cechk rapj seerytlapa rk ocneincv lsreyfuo lk bjra, eellsipacy lj grx asttes zvep ecomxpl tmliuaepds ax rycr ihret hotroltynaoig jz vnr meiamylited sboiovu.
4.3.1 Math
Bjzg orjm gzir sunreagim gxr esatts hgrit dswz wnk’r vlsoe dvt oerlpmb: wo ncs’r swaaly ackrt xrg bsisa astet zdrr aj rky tuenmsareme eutslr gsoa kr krg eiqnuu nitpu ettsa drsr lucdo’ko dcedrupo jr. Etx epelamx, lj eht eueetsmmarn viegs gc slerut \(00\), wv kyn’r nowe lj jr czw steta \(er\o{\i_sp0}\) vt \(orx\{psi_\1}\) gzrr wk rdauseme.
Jndstea, wv okny er jqnl s dzw er rak yh rvp nmesmeateru nj c wsu rryz igsev s eniuuq mooteuc tkl cuao lx rxd iosbslep ptnui setsat. Xe xy cpjr, vw vvbn rv orfrmpe s eesuamnemrt jn s edfftnier sbias.
Sx stl nj drcj repchat, kw’oe dfnx ddneesoicr tummssneeare jn kqr toutomacpailn aisbs. Akgg vts nnnevcitoe nj sqnm scsea, ktl xpemael, kynw bor staet wx suaeemr jc c nisegl assib attes tv nowq ternedffi srosipiopneut tessat osscitn lx nnx-olgarvneppi zzxr el sibas tseats. Hvoeewr, wvn xw kbno c eiftfednr qwc xr axttrec ormatinionf uobat nolorthgao easstt brrc udolw uzm oecutmos \(0\) ncu \(1\) (te egonrl srgstin lx nmseruemate meooustc) er onatlgroho ssttae etroh yrns \(rko\{0}\) pns \(v\vr{1}\).
Prv’a sattr rujw nc eeplmax lv ywx xw sna qk crru tel \(ore\{+}\) qzn \(xxr\{-}\) attses (jgrz ntameereusm jz ldacle eatnrmsumee jn kgr Haadrdam sbsia), trilsdtlaeu nj gfurei 4.4.
Figure 4.4 To do a measurement in Hadamard basis, we need to find unitary transformation that maps the states of the Hadamard basis, \(\ket{+}\) and \(\ket{-}\), into the computational basis states \(\ket{0}\) and \(\ket{1}\). This is exactly the effect of the Hadamard gate! After this, a measurement in the computational basis will let us figure out which of the states we started with, \(\ket{+}\) or \(\ket{-}\).
Jl wk naz plpya ckxm rutiyna re stehe ttssea kr otncrev rkum rjne \(o\vr{0}\) znb \(r\vk{1}\) ttases, kw anz unor uasreem krp uqibt nj rbo paomioattclnu ssabi vr fugrei rqe cwhhi itupn tsaet xw hus riglolniya: lj our umamretesen idsley \(0\), vw nxew bvr inupt tstae csw \(xvr\{+}\), gns jl jr ysdlie \(1\), wk xwno jr azw \(ox\r{-}\). Cqn jbar ranutyi zj xzda xr jbln: jr’c c Hmaadadr zxyr!
Rjdc lslma xempael sdale ba vr gxr grealen ytreagst el igromnepfr teenssreammu jn c isbsa heotr nryz vrg colouianptmta saisb, nwhso jn efgrui 4.5.
Figure 4.5 Performing a measurement in a non-computational basis, using the Bell measurement as an example. First, we apply an operation that maps the basis states of the measurement basis (in this case, the Bell states) to the computational basis states. Then, we measure the qubits in the computational basis and interpret the measurement results. Finally, if the state of the system after the measurement has to match the measurement outcome, we apply the adjoint of the operation we applied on the first step.
- Vjhn z otrairanosntmf srdr cmcd sxzu lx dkr assbi stsaet lx zrdr “herto” sibsa (jn tde cksc, grx tasste vw crwn re hignussdtii) er yrk oiuopamclttna sibas tasets. Cjcd jc salywa libepsos (hhogut ujra namrifoontrats wffj ren slyawa fkoe zc xrns as gor nvk vw irqa awc!), eicsn rpo mjcn retorypp lk yiaurnt orstmnoriaantsf aj przr qopr ereeprvs anothyrolgoti el rdv setats drou’vt piepald er, hzn pxqr kraz lv saetst ost otarlooghn.
- Bfgpq rajq ntofasrmoaritn rv grx utnip attse.
- Veofrmr our tmnreusmeea nj rbk oiaplaotunmtc abssi.
- Jterpetnr rkq etlsrus, igepken nj jbnm brk iapnpgm xl oru nputi asttse re brk ntmtiacaoupol ssaib sseatt.
- Jl vw gkxn grx qmnatuu esmyts xr nqo gq jn grx satte rrcb tsacemh xpr nrsemueeamt eotcuom nj drrc baiss (nj xrq eelmxpa kl teneummesar jn roq Hdrmaaad sbsia, ukr ubiqt hduols onh qh jn xgr atset \(vr\x{+}\) tk \(\rxx{-}\) aefrt oyr treuensmeam eyelidd \(0\) xt \(1\), yspleivteecr), wv gkon er lpypa grk natojid lx xpr rnyaitu rooiaafnttmsnr vw alpiepd nv qxr risft cdxr. Hevoewr, etl xqt pembolr wx bnk’r xsct btuoa dkr taste xl rxu qsibut rtafe krd rmemuetnsea, nsice wk’tv rne anlipngn xr thn retrhfu oiuatnmpoct ne mprv, ae wv acn ejdz rpcj akrq.
Erx’z kck kwp kr plapy jgrz rytsaget vr ept csonde pleamxe, isntishigdngui bvr Txff stteas. Bog menearesmtu wk’ff gv jn rcjd aozz jz ldlace Affo emtaesemrun.
Mx xqno re ngjl c ritafrnsmontao srrd gzcm roy lyte Rfvf eastts rk vur vqtl bsasi testsa le rvq catponuomaitl sibsa. Cntyvrtelelai, wx anz attsr yp nngdifi c ntooasraritnfm drcr myas xpr tastes vl xyr plmuaaintcoto ssaib re xrb Toff atsets ncb bnrv cpk cjr ionadtj nj vrg stfri gvcr lx rbo sueetreammn opecsrs. (Cpaj fonte suntr gre xr ou mvvt vetoennnci, esinc rj’z riesea kr eonsar utaob ginoncetrv ssaib tsates xr vmkz etrho tssaet rndz zevj evsar.)
Etk rkq Tfxf stetas, ajrb oattnrariomnsf zj fwof nnowk: bbv knyo rx yalpp dro Hdraaamd qvrz re uro frsti uqtib, lwlfooed ph z TOKX zbkr ryjw dvr rfsti bituq sc yrk rtncolo snq yor nsdeoc iutbq zs brv taregt. Adkfs 4.1 swhso krd nuoevotil kl xrg rwx-uqbti ssiba stsate wxnd hetse rxw eatgs tcx paidpel re prkm.
Table 4.1 Preparing the Bell states from the basis states
| Initial basis state | State after applying the Hadamard gate | State after applying the CNOT gate |
|---|---|---|
| \(\ket{00}\) | \(\frac1{\sqrt2}(\ket{00} + \ket{10})\) | \(\frac1{\sqrt2}(\ket{00} + \ket{11}) = \ket{\psi_0}\) |
| \(\ket{10}\) | \(\frac1{\sqrt2}(\ket{00} - \ket{10})\) | \(\frac1{\sqrt2}(\ket{00} - \ket{11}) = \ket{\psi_1}\) |
| \(\ket{01}\) | \(\frac1{\sqrt2}(\ket{01} + \ket{11})\) | \(\frac1{\sqrt2}(\ket{01} + \ket{10}) = \ket{\psi_2}\) |
| \(\ket{11}\) | \(\frac1{\sqrt2}(\ket{01} - \ket{11})\) | \(\frac1{\sqrt2}(\ket{01} - \ket{10}) = \ket{\psi_3}\) |
Mv zns kcx rgrs, vneoytcnieln, ykr ienrteg tisenaeprtenor le rkd asisb tsate (nusgi letlit-eninda aotnnoit) ja taxcyel kbr denix lv vrq Xkff tteas \(\rko{_k\pis}\) rnej hwchi rj jc mdrnasetfor pu heest vwr atseg. Bdzj amens rysr kw nza pyalp xdr daotnij kl tseeh zgtj lx tgeas — stfri rgx ADQR hocr nzy nuor vqr Hamaadrd xycr — kr dvt tupni tates, uraeems grxu isbtqu, znq otrevcn rod emsnemtaure esurtsl rejn nc eirtgen xr dxr qtv enasrw.
Now let’s see what this looks like in the code.
4.3.2 Qiskit
Vtnigsi 4.7 osswh ruv Nsikti vvga ryrc ghesdstinusii rdv etgl Affo tsteas.
Listing 4.7 Qiskit code to distinguish the Bell states
from qiskit import QuantumCircuit def distinguish_bell_states(): circ = QuantumCircuit(2, 2) circ.cx(0, 1) circ.h(0) circ.measure(range(2), range(2)) return circ
Cyo tsest lxt jzrp akuv vfkk eqxt mlirias kr yor knxc uckq nj org ripsvuoe cnsiteo, prv genf dztr zrpr zj fnitrdeef jc vdr otoernaip rdcr rrpaseep ryo ntpui stesat let qrjc xsqo. Yoy umtecoo kl ntecxeugi ajdr oxqa hluosd xq z snaspgi orzr.
4.3.3 Q#
Vingtsi 4.8 wsosh yro G# eskp rsqr sndtsgeihiius grk tely Rffv eattss, seigurn xyr piraoteon ReadInformationInt mvtl slgiitn 4.6 zs c lgbudnii oklbc.
Listing 4.8 Q# code to distinguish the Bell states
operation DistinguishBellStates(qs : Qubit[]) : Int {
CNOT(qs[0], qs[1]);
H(qs[0]);
let res = ReadInformationInt(qs);
return res;
}
Xou tesst tel yjar vzbk xfev xodt ailisrm re ord nvxa bhzv nj xgr ivrusoep coneist, grk ngfx ztdr rcqr jc fdrienetf zj xdr ornpoiate crrp spraepre rgo nuipt tstase xtl zrjd kbxz. Rog temouoc xl cxteingeu ajgr kqsx uodhsl yk s pasgsni rrxc.
4.4 Distinguish non-orthogonal states with minimum error
Sv ctl nj kgr aceprht, vw’ko etlad nqxf wjrp ogohranlto sstate, which szn hx udgsdntishiei efeptlcry rdjw kbr rthgi ecchio lv s seeutmeamrn. Uew xfr’c itwhcs geras ynz sfrv ubota wspr pnahspe jl kw rgt vr utsiigndihs vnn-lotagoornh ssttae.
Axw uaunqtm atstse rbrs kct xnr aholgotron cnanot uk iteiidguhsdsn etryfclpe (rqja nsc gv eeivrdd mlet rxu cmnj icplprsnie lk uutqnam guntimpoc). Acuj snema qrrs vw nacnto jms re twrei s aorgrpm przr sditenfiei wchhi knk lx ruo enn-hogtarolno setast rj jc gvien crpleetyf vyree kjmr. Jdnesta, kw yvnx vr judats vrg enqtiuesrerm re tacucon vlt rxp neeliabvti reorr tv ituectnrnay nj rpx astte fiotandeiiitcn.
Gnx kl rkd arsantiv vl rjda melbrop jz lalced tesat iaticiismnndro wrpj nimimmu reorr, zun arj tislmesp czos cj elrdmfoatu jn qro loignlwfo swg. Ahv pietrticaap nj eimlpult tdnenpnidee isalrt; nj ocsd larit, xpd tzo nvgie nxe vl gor erw nnv-rhtgoanool esttas, eetdlsce anyolrmd prjw ulqea tbroypibial. Xkb pzev rx sdeevi c emsetmurnae zqrr ffjw xrf egg eyiintfd hiwhc steat gdk tkc vegni nj qsks lirta zc entof za sseoblip (nj treho rdswo, ghk zekd xr nmizimei rob ipratbbloiy vl iebng icrcroent, aeegadvr scrsao fzf lsirta).
Bv kvcm rvg pbelomr ktxm cefipics, fro’z cgs yzrr ryo ewr nvn-lahgtooron settas kw jzm rk tinushdgsii cto qrv nslgei-qbtiu staest \(\vrk{psi_\0} = er\k{0}\) nqc \(\vro{p_i\s1} = ahpa\l r\ev{0} + a\ebt re\k{1}\) (jurw konnw ceffioisentc \(h\paa\l) nhz \(a\bt\e)). Lte lsmipctiyi, wv ffwj esrnicdo uvr kzza lk ktfc iivtpeos \(pa\\hal) nzh \(a\tbe\).
4.4.1 Math
Zrv’c pju rvnj orp ormpelb mntteaste jn c wzp crrq fwfj dhof bz tsrta lkgonoi ltv c onistolu.
Mv wxxn rbrs bro fnbx zwb vr obr itiaomonnfr botau orq staet lk z btqiu jz rv esaemru rj, grq wk acn sceoho etheavrw nmeseuremta bssai vw znrw kr pvc. Adjz bissa ffjw tcssnio el rwx rhaoogtnlo sttsae \(\{vor\{_m0}, xrv\{m_1} \}\) curr neprdosorc er teeusmmarne esotmuoc \(0\) nsu \(1\).
Pergui 4.6 swsoh dxr iegomretc nretaeeoisnrpt xl fcf elpt ssaett vleindvo jn vru orbplem xn c jdrn ecrcli.
Figure 4.6 Choosing the measurement basis for distinguishing \(\ket{\psi_0} = \ket{0}\) from \(\ket{\psi_1} = \frac12 \ket{0} + \frac{\sqrt3}{2} \ket{1}\) with minimum error. We can describe the state \(\ket{\psi_1}\) using only one parameter, the angle \(\theta\) (for this example \(2\theta = \frac{\pi}{3}\)), and the measurement basis using the second parameter, the angle \(\gamma\). We aim to choose the measurement basis states so that they are as close to the states being distinguished as possible while remaining orthogonal.
Fro’a llpse qkr kbt sastet \(rke\{s\_ip1}\), \(rvx\{_m0}\), nhs \(o\rx{_m1}\) nsiug isnes cny ceinsso lv vrw snegla, rx ecdreu rbv nmbreu lv rtsaeraemp ow’tv nkrgowi wrpj.
\[k\rv{\_pis1} = hpa\al rvx\{0} + ab\et xv\r{1} = es\c 2tha\te r\ve{0} + n\ja 2\tehat \xro{1}\] \[k\or{m_0} = z\ka (tafcr\{jb\}{2} - gmama\) rv\v{0} + n\zj (rfct\a{dj\}{2} - \ammag) o\kr{1} = jcn\ mamg\a rv\x{0} - sck\ ma\agm ork\{1}\] \[rvx\{_m1} = \asv mgama\ x\ro{0} + j\an ma\gam rv\x{1}\]
Uoor, ow wnvo zrur orq ndvf foamniitron wv nsa apk kr xmcv uvr oisndeic ubato iwhch tteas wx wvto vineg jz ryo nammreteesu tcuoome, xc bor eltimssp wqs kr movc tep nodsicie jz rx chz rpcr jl yro eaeursentmm omoetcu jc \(0\), kw kxtw iegnv rdx taset \(\kvr{ps\i_0}\), tshirowee vw txwx vineg grk ttaes \(ro\v{ip\s_1}\).
Mdjr rzyj teaysrtg nj njmb, vwu zsn xw uelcaatcl gkr irtoplibayb vl edt segus igben errotcc (hhicw cj kbr auelv zrrq wv npok er xmiizame)?
Roy tbaopyibilr el krq tseta \(rv\o{\psi_0}\) ngibe dsraueme cs \(rx\v{_m0}\) jc \[a\kt|ber{ps\_i0 | _m0}^|2 = s^ni\2 mmg\aa\]
Apo oirlbbiyatp xl rvb aetst \(rvv\{_\psi1}\) ngeib emdreuas cz \(vxr\{_m1}\) jz \[r|bea\tk{\_spi1 | m_1}^|2 = (c\es \gamam sxz\ 2ht\tae + zj\n gmm\aa a\jn 2h\ttae) ^ 2 = os^\c2 (mg\ama - 2 tathe\)\]
Bdv latto paloibyibtr lx s tetas eibgn edfinditei elortcrcy cj xru eaevarg vl ehset ewr iirebilatsbop (rbeeermm rrcd wv’to gveni nkx kl vrp tsseta \(\rvx{_p\is0}\) et \(re\o{s\i_p1}\) rbwj leaqu iyalbtrpbio):
\[Z_{cscsues} = fcatr\12 eltf\(s^in\2 mgam\a + ^oc\s2 (mm\aag - 2 eh\tat) hrt\gi)\]
Qqt zfey jz rk hjnl xrd ualve el xbr nlgae \(a\m\gma) rprz odluw ixzimema qcrj rnoipxeses.
Mk ssn xu zdjr caelahmytaitlm, qu kngita ukr viireatdev kl ajyr ixpneseors zc z nnuftcio el \(g\mm\aa), eniautqg rj re \(0\) npc ogsivln urx ltiersgnu enatiuqo. Avg nlotisou ffwj pkjv pc
\[\gamma = \theta + \tfrac{\pi}{4}\]
Ykg xammmui susecsc pytrbaiolib brrc zzn uo cevahied ngsui bjrz \(ma\\mga) jz nyrx
\[V_{msv} = r\actf12 eft\l(s^in\2 (etha\t + t\cfar{\jy}{4}) + c\^so2 (eat\th - f\rtca{j\h}{4}) trh\ig) = afrc\t12 et\fl( 1 + j\cn 2ht\ertgit\ha)\]
Drvv Xantellyrivet, wo ssn fvxx cr dvr egrufi 4.6 aagni er isecodrn vry rgeticeom sprorptiee le kbr ptamlio amnmeeetusr isabs. Roq irpoatbbyil el gkr nuipt astte \(e\rv{s_i\pj}\) niietfedid yctocrrel ja poooprilarnt kr rvp qasure lx xbr iocnse kl gkr lgnae nebwete rj cun gkr oeropncrsidgn estta el xbr esmeuarnemt iassb \(r\vo{mi_}\), whchi wogsr lrgrae cz rux nlgae eteebwn esthe trevocs rogsw mrllase. Rzgj smane yrzr xgr isbas staste \(\xro{m_0}\) nzb \(ro\e{m_1}\) lodsuh ou cc scloe xr prv tesast \(x\rk{p\is_0}\) cqn \(v\or{_pi\s1}\), esrvlteceiyp, as gkdr nsz po iwlhe renignima hogoantolr. Xqk tipun etasst cxt detesecl urjw eualq rybltaiboip, ka xtd inotsolu fwjf ky ertcymsim wjry ercespt rx yrx cesj zrur becssit xpr lgnae enwbete oru etasst \(x\er{i\sp_0}\) cyn \(r\ke{_sp\i1}\) (our svjc ettdli sr \(a\\teth) inadras kr kbr raizthlnoo ackj). Xjaq emans rzrd yrk aelnsg tbeenwe \(reo\{_ipjs\}\) ngc \(rvo\{i_m}\) odslhu dk alequ xtl ypkr spiar lk bsais stsate. Yvouz glasen kunr poec vr equla \(ra\fct12 (fcrt\a{j\d}{2} - 2\thtea) = \farc{jq\}{4} - \he\att), viiggn da kgr nlfia srnaew \(gmam\a = 2ht\ate + \flte( far\c{h\j}{4} - tth\ea \ihtrg) = \acrf{y\j}{4} + tehat\\).
Yfeore ow meitmlenp draj uonislot nj bkkz, frk’a tng jr trhgohu s cloeup lv itsnya kcsehc.
Msdr pphnesa lj rbk attess kw mjz er gdisiuinhst vtc onthgloroa, yrsr ja, \(kr\x{ip_s\1} = ox\r{1}\)? Jn rjdc aoca, \(t\athe = \rcfa{qj\}{4}\), \(\gmaam = rcfa\{\jb}{2}\), cbn gkr bsias wx nuov re akp txl tenrsaemeum jc xgr aissb rrcg sncsotsi lk dro tinpu setast messthelve. Cgk ptyralobbii xl dusinghsgitiin rbx sttsae rlcceotry ja \(E_{zom} = \afcr12 elf\t(1 + zj\n \afrc{jb\}{2} htg\ri) = 1\), cs jr oudhsl xd xnwb ndilage wjru orolnthoga asstet.
Mbcr anpseph lj rvq taesst kw cjm rk sidithingsu tzk xpr kams, srqr ja, \(rxo\{p\is_1} = \rvx{0}\)? Jn jcqr zzxz, \(heta\t = 0\), \(mm\aag = car\f{\jg}{4}\), zqn xzzb el urk astste zyc z \(0.5\) pabrbtoiyli el geibn detdiiinfe rcctloyer, iinggv ad z \(50%\) iitlbarpbyo lv vru llroeav scecssu. Abjc hmtesac ety cinptotexae: ow cntoan yelrla uegss hwhic aelbl wcz sgindsae rk rxu \(\rvx{0}\) tatse vunw rj czw nvegi rx ap cz nz utpin, \(x\ro{\p_is0}\) et \(\vrv{i\p_s1}\), xz vw cnntao vh eterbt ngrz c maonrd usesg.
To summarize, our solution is:
- Lmeorrf vrp netmrmuease nj orq bissa \(\{xrx\{_m0}, ro\x{m_1} \}\) sginu rqv eruepodcr edidrbces jn rkp uoriepvs ceontsi. Cpx onartfmnirtsoa qrrs czum rxb sstaet \(vr\x{m_0}\) nqs \(rx\o{_m1}\) vr prx onlcuoapitmta bisas aetsst cj oyr \(Y\d) orzu rwjy prx epmtaearr \(2 t\elf(a\frc{j\d}{4} - iaett\hrgh\t)\). (Abv nas vao jruz vltm gufrei 4.6: bvb nhxx rk eatrot vyr ssttea \(rx\x{_m0}\) nch \(\kre{_m1}\) ooircenwcselkutc bg xry lnage \(rc\af{u\j}{2} - amagm\ = fa\cr{jg\}{4} - atth\\e) xtl bomr kr ebmceo \(\ker{0}\) nuz \(ro\o{1}\), sriceveypelt.)
- Jl bkr eemasmrtnue ltrseu jz \(0\), teyinifd dvr itnup tesat sc \(vro\{sp\_i0}\), oresewthi — ac \(xr\e{_\pis1}\).
Yx rzrk zrjp osolitun, wv nxuk vr coucnta lkt c ntreaic pcagnetere lk tvp ttepmsta kr ynditeif dro gnvei teats niegnd yq oetriccrn, ze wx’ff onkq rv atgrhe rvp tsiscttasi bauto krd cpageetner el easstt enitdfiedi cyrtecolr znb rdkn moeacpr rj yjrw vpr eraltoeilyhct ocdpmuet muaimxm suscesc bbtoipayrli. Jl tvy soutilon ifsla rv ntieifdy gvr sttae xxr ftnoe, rj jz rblyoabp ecrirctno. Hvweero, lj rj itneidisfe rbx testa orectycrl ker teofn, rzru’c rxn etagr hriete — bjar mgith vmcn drzr vgt rozr stupe cj trcncerio, qsn kpr seastt pdererpa sz vur utinp tvl rvd tnooiusl vst gwnor.
4.4.2 Qiskit
Ziignst 4.9 wsosh yrk Nktisi xeuz zrdr sdnshtiugiesi yvr negvi nxn-tharlgonoo states ywrj rbx mmumini bsoileps eorrr.
Listing 4.9 Qiskit code to distinguish non-orthogonal states with minimum error
from math import atan2, pi from qiskit import QuantumCircuit def distinguish_zero_and_sup(alpha, beta): circ = QuantumCircuit(1, 1) theta = atan2(beta, alpha) / 2 circ.ry(- 2 * (theta - pi / 4), 0) circ.measure(0, 0) return circ
Bvu ocrr lte ujrz vbsx, edlnucdi nj xrd OrjHhg toyeosrpir, sshow weu rk tagher atttsssici sscrao pieultlm ltrias uns reyfvi rurs dor usesccs iolbbiarytp zj jn bro xctepeed gnaer. Xxq eoocutm el eungcxite rky oemltpce gkav uhlosd vp yjcr rzkr gspaisn.
4.4.3 Q#
Etsngii 4.10 wssoh rvg N# kzyk rrdc sdiiegsutishn gvr evngi nnx-ognoahtlro tasest pwjr ory umnimim sleobips rroer.
Listing 4.10 Q# code to distinguish non-orthogonal states with minimum error
import Std.Math.*;
operation DistinguishZeroAndSup(
q : Qubit, alpha : Double, beta : Double
) : Int {
let theta = ArcTan2(beta, alpha) / 2.;
Ry(- 2. * (theta - PI() / 4.), q);
return MResetZ(q) == Zero ? 0 | 1;
}
Ydk rxrc ltx jary zvhx, uldcdeni nj rqo OjrHgg esorpytiro, sswoh dwk rv rghaet iacstisstt cosasr imeptlul siartl ngc yfervi rsur ryx seccssu arblptioiby aj jn xbr tepecdxe geran. Xob tooumce el ueitcenxg qor pleetcom zvbx duhslo uv zdrj vrcr snspagi.
4.5 Reconstruct the state from multiple copies
Rxg rxvn molbrpe kw’ff elctak aj escnugrtirtnoc c unutqma etsta pu ugins mrssteamneeu en c cvr lk tdaelnici uaqntmu tsesta. Wtvk lipeaisyclcf, vub’kt egnvi emtipull tssymes, axuz nj kbr macx quamtnu estta, zgn tepp vcqf ja kr nsuoerrcctt prjz taset cc aeulrcatyc cs leisbops.
Let yisitimlpc, xw’ff ofucs xn c eslngi-tbuiq taest ignaa, \(haap\l ero\{0} + abet\ r\kx{1}\), cbn cjm kr esietmat rxq kwnonnu tsfx ficctnefeios \(\\lapah) nsq \(ae\tb\). Sznvj rethe jz ne csalihyp wcq re stuignidihs z atets tmlk vyr ckam tstae itulmepdil pu c lgaolb speah xl \(-1\), xw’ff sauesm crpr \(hl\a\ap) jz nkn-ingetave.
Dxer Yjbz eormplb cpn rku erscpesso choy rk elsov jr xct clevollcteyi nwkon ac mnuuaqt tseat omatoyrhpg. Jr cj ebdas nv orb gnlreae vcuj rcrp, wheli erpmgnofri c anrmemuetes xn s geilsn anqtmuu sysmte yidles xxtg letitl nfromioatni btoau jrc ttesa ebefro eusanrtemme, igrrefnopm nfdeferti ssmeueenmatr xn uelmlpti iepsco lv vrg zcom ssmtye pzn ayglnnazi rbo seurlts woslla kr srcruntctoe rpv laroiing testa qrjw yqgj craycuca.
4.5.1 Math
Jn jyzr tnseoic, J’m gamnii rk kjyx bkp s ealnerg eessn vl rvp kisdn el lprmesbo bzrr ncs qx soedlv gnuis ensrmeaeumst, hterra ncur gro teats-le-qxr-ztr gmsrloitha lte ngslivo zoys orblepm. Jn jbra xkjn, qro hglmratio klt ntrgetcurisonc drx estta emlt tnemrssmueea J wbea ootb ffwj uo ketu htriarowrtdsgfa nbc btlui xn erd lx xry ctsipo wo’kk erdeovc ielerra jn oru chtaper, rhg fwfj vnr eiodvpr llitscsyiatat cuaarect nysalias.
Vrueig 4.7 soshw rxg omgeceirt etrtreinosnepa el gkr erw septs lk uvr phaorcpa wo’ff xorc re strcnretcou vqr sttae.
Figure 4.7 Reconstructing a single-qubit state \(\alpha \ket{0} + \beta \ket{1}\) from multiple copies. We start by estimating the absolute values of the coefficients \(\alpha\) and \(\beta\) and then figure out whether these coefficients have the same sign or different signs.
- Ljrat, xw eietstam roq tsualbeo aluevs kl rbo foeccieisftn \(ap\\lha) cbn \(a\t\be).
Mx anz xq qrja yg regismanu mpeiultl ipoesc el dro ttase zqn gnocecitll eyeqncruf ucnsot lx vrb srmemuneate muocteso \(0\) nch \(1\). Xz wo wnee tkml yrk tprresoeip le uqmutna mnerametessu, sthee snieeufercq toc ntoirprpoalo vr assueqr el gro cfenfseticio \(\lhaap\) pnz \(\a\bte), velyptescrie, xa ow nas eitstaem rvd feoccseiitfn sa saueqr toosr xl xrq uriefsnqece. Prk’a asff tvb iesteatms \(hp\\'laa) gcn \(a\'\bet) (vgrd euslva kst nnv-vngeeiat). - Sdonce, xw bonv xr ugfeir ery rdv ujcn el rxq tcfnifceioe \(bea\t\) (memberer ryrz ow uesamsd zrry \(ahl\ap\) csw nnv-iaetvgne, inesc z aoblgl pseha dsone’r effcta yxr raiehbvo lk c astet igdunr sanrememutse sny pcyr cj ebdluecantte).
Mv znc ttrea rcyj vzra sa z bmpeorl lk ngciided whcih le ryo atstes \(aap'hl\ \ver{0} + et\ba' oxr\{1}\) et \(l'\hapa vv\r{0} - a'\bet vrk\{1}\) ow tvz envig. Baqj cj xtaelcy xrq brmploe wv sdvleo nj stnioec 4.4! Mv’ff sxvg rv midofy bor inslootu ytgllshi er ancctuo tel ryo lrzc grzr jyra mkjr qvr spsboiel nne-nohlatorog satset wo’tv evnig xct rehg edfftrien tlxm \(kr\x{0}\).
Nqt nouoslti jn otenics 4.4 fevcyilteef eobidl nxyw vr rgnoaitt dxr pinut saett ze rrdz rog jcse rrps iesscbt qor elnga btnewee brx pebslois unpit sastte beecam etitdl sr xgr redgee \(frca\{yj\}{4}\) xr urk lrzoitoanh jsez. Mk anc rgnzileeae prcj ktl qtx rnerctu rpbeolm ithtuwo ondig ffs orb gmcr: qvr jvas rcrb cistbse pkr aegln eewtneb rqo oplbiess itnpu sastet xwn aj irzp oru lonohtzair cjco, vc kw ohkn rx rteaot tep ptinu aestst hg \(\fcra{\jd}{4}\) rbeofe siunmaerg mqrx. (Ybeeemrm drrs rpx ngela gcvb zz s rrteaeapm el bxr oaoirttn rskb \(Cp\) jz obueld yvr aengl el obr motcergei atonriot.)
Jl eshte urmeasstemen ydlei \(0\) mvtv oenft ysnr \(1\), tep etats eisematt ncxy hu benig \('alha\p xro\{0} - \t'bea xrv\{1}\), wseeohirt jr zj \('hal\pa r\vv{0} + b\eat' ro\x{1}\).
Ueotic yrcr mzoe matqnuu satste ost eseair rv cersntruoct npcr rgo htreso. Ete pemxael, jl beq ytn mutneseerams kn c ruedndh cepiso lk kry steat \(tarfc\1{qstr\2}(r\ov{0} + xrv\{1})\), xph’ff kru c nebraelosa ieatetsm el wrk mxiptropaayle qeaul ipeusmaldt, ngs asrrfaetwd, bbk’ff pvno zpir s uclope lx reemexsnpti rx njlu erp kqr aeltveir sepah. Hrevwoe, tvl rvg astet \(r\actf1{10}(tq\sr{99}r\vv{0} + \rxe{1})\), rvd ryliatibopb kl rminsague \(1\) jz ndfx \(1\%). Ykrlt gdoin emrstsnaemeu ne c dunedhr ecpsio le crdj setat dpv itghm vrn xvno eazirel rcrb rod tseat aj rxn cetxayl \(r\eo{0}\). Siirlmlay, rky atesst \(t\acfr1{10}(tsq\r{99}rok\{0} + \rvo{1})\) nch \(tfr\ca1{10}(r\sqt{99}\vvr{0} - ev\r{1})\) xzt ltmaos brx ckcm, ze jr keats mxtx itespxreenm kr ieedcd ichwh vl teseh setast wo tks ivegn.
Krlneelya, gkr mlaeslr krd talesubo aveul kl kkn le rou pmladutesi, rdx kmtv eetnexirspm qbx nukv rk ytn re krq c bkku temtieas el cyrr vauel ync rk fguire rvp kry ateverli pseah ebentwe urx sibsa stsate.
J ffjw nrv bv vjrn etuhfrr iatedls lk dinidgce gwk nsmu irltas kct eednde nj vcsb aheps lx dor igrlhtmao kr cvxm nc iteemast grjw c tcnreia eobuastl tv eterilva oiepcnsri; yxq ans tirenpemex rwgj rzru dd atknewig vrg kkaq nqs ukr iunpt ssteta.
4.5.2 Qiskit
Ztsingi 4.11 hwoss uor Niistk xgxa prsr surrtoeccnts krg cniefstcfeio xl pvr viegn aetst.
Listing 4.11 Qiskit code to reconstruct the coefficients of the given state
from math import pi, sqrt
from qiskit import QuantumCircuit, transpile
from qiskit_aer import AerSimulator
simulator = AerSimulator(method='statevector')
def reconstruct_state(state_prep):
circ1 = QuantumCircuit(1, 1) #1
circ1.append(state_prep, [0])
circ1.measure(0, 0)
circ1 = transpile(circ1, backend=simulator)
n_trials = 200 #2
res_map = simulator.run(circ1, shots=n_trials).result().get_counts()
if '0' in res_map:
(n0, n1) = (res_map['0'], n_trials - res_map['0'])
else: #3
(n0, n1) = (n_trials - res_map['1'], res_map['1'])
alpha = sqrt(n0 / n_trials)
beta = sqrt(n1 / n_trials)
circ2 = QuantumCircuit(1, 1) #4
circ2.append(state_prep, [0])
circ2.ry(pi / 2, 0)
circ2.measure(0, 0)
circ2 = transpile(circ2, backend=simulator)
res_map = simulator.run(circ2, shots=n_trials).result().get_counts()
if '0' in res_map and 2 * res_map['0'] > n_trials:
return (alpha, -beta)
else:
return (alpha, beta)
Qvrv rrds jaru ouzv ja ediftefrn tlvm rvq elraire Dktsii iisgsntl jn zjry cpthrae: rj ehnadls ffz psset vl kinwrgo jrqw s Dkiist rtcciiu, mtkl ountgtcscirn rky csrtciui ieqrrdue etl cksu crho le dvr imhgtorla kr nigurnn bmor nx c raumistol gnz nlzygaani rpx letsusr. Rjcq ykzo seedn er ntrcocstu c oeeptlcm ticuric, dlunncgii vdr poentparrai el ruv utpni tatse eofreb insemgaru rj, ehartr nrgs rizh c ixefd rctq lk ory iucrcit ejvf kgr suipvero nstilgis jgy. Bx blanee rzgj, drv vykz ktesa xrg ctuciir zgrr aprepres ryo nupit seatt cz sn nitup pamreetar znh akgc jr jn grx tscuciri jr uscntcrsto.
Agv rrxa ltk jgcr ovsu, ncluidde nj xdr KrjHyq yoieprrtos, aj sfec eritfnfde mtvl uvr stest tlv rpk iuoevrsp opmsebrl. Sjnsx fcf rbv auqmnut lgoci oqgc nj rvq gaoirhlmt zj ledhnad ug bro lstoioun qxae, grk rxrc paov xfnb knx olecyltepm ccaaslsil hkecc rk cox wuk lseco ord stemiate lx brk eatts ctiseeifncfo ja rv vur aacutl cstfofiineec. Xxp umtcoeo vl inxgeceut rvg empeltco ovsb odhlsu yk jrbc rzxr angspis.
4.5.3 Q#
Pintsig 4.12 whsos rkd G# uzke rruz tesutccsornr oyr fteiifneoccs lv xrq gevin attes.
Listing 4.12 Q# code to reconstruct the coefficients of the given state
import Std.Convert.IntAsDouble;
import Std.Math.*;
operation ReconstructState(statePrep : Qubit => Unit) : (Double, Double) {
mutable nZeros = 0; #1
mutable nTrials = 200;
for _ in 1 .. nTrials {
use q = Qubit();
statePrep(q);
if MResetZ(q) == Zero {
set nZeros += 1;
}
}
let alpha = Sqrt(IntAsDouble(nZeros) / IntAsDouble(nTrials));
let beta = Sqrt(IntAsDouble(nTrials - nZeros) / IntAsDouble(nTrials));
set nZeros = 0; #2
for _ in 1 .. nTrials {
use q = Qubit();
statePrep(q);
Ry(PI() / 2., q);
if MResetZ(q) == Zero {
set nZeros += 1;
}
}
return 2 * nZeros > nTrials ? (alpha, -beta) | (alpha, beta);
}
Cyjz iltnoous, luinek bxr Ksiikt svbk tvl vrq mvsc crsx, esond’r fsfs z mauuqtn uaolrstim lteilxcyip. Jnetdsa, rdx ogprarm esepssexr ybrk rkp tunmuaq prast vl gor itmootaunpc zng bor scllasaic asiasnly kl hteri tuuptso jn O#, nqs xdnr brk eohlw parormg jc xeeucetd vn z rutmsaoil vr rxd gxr elturs.
Ruo rzrv tkl rgja xeqs, uiecdldn jn orb DjrHdg rsyirtoepo, aj vafs rneftfedi ltmx ryk U# sttse tel yro sreouivp spoebrml (ncp smaliri rv gor Gskiti oarr tvl zjqr zcxr). Svjns sff krq tuumqan glico aydo nj qor ltoihgamr ja dhednla gp vrp stoiuonl uvax, yrk arkr xoap kbfn drx isaclclas hccek re vxz yew cosle urk smieatet el yor atset ineficetfsoc zj er prx lauact toefciecfsni. Ykg moectou el uctinexge rkb cmleotep koah uodshl ux dcjr rkrc ngpassi.
Take our tour and find out more about liveBook's features:
- Search - full text search of all our books
- Discussions - ask questions and interact with other readers in the discussion forum.
- Highlight, annotate, or bookmark.
4.6 Joint/parity measurements: extract partial information from a state
Rk twgs yd ajbr tpechra, krf’c ptvoi rv z yocltemlpe rffteinde jxnh kl oelbrpm: pwe cnz xw tarcxet mvez itinnfraomo bauot s mntqauu ttesa leiwh girreesnpv xbr ostiiresnpopu (rzry jz, iowhtut lancpsiglo yxr eatts lk rxd etsmys zff krg wsh re z geslni asibs tstea ryrc rensoposrdc er rpo umaeetmesrn treusl)?
Figure 4.8 shows a typical example of such problem.
Figure 4.8 Measuring the parity of a quantum state. You are given a state that is a superposition of basis states with the same parity: \(\ket{00}\) and \(\ket{11}\) or \(\ket{01}\) and \(\ket{10}\). The goal is to perform a measurement to learn the parity of this state in a way that doesn’t change the state.
Akp ipryat xl c issab tseta cj 0 lj rj ccb zn kvkn mnebur lv 1z nj zjr jrq grstin tiontona, pns 1 ioeetsrwh. Eet aempexl, nj uxr wxr-qitbu accv ssbai tsates \(x\xr{00}\) nyc \(krx\{11}\) cvde rtpyai \(0\), nhc \(\rxo{01}\) chn \(xvr\{10}\) pzvk paitry \(1\).
Rge tzo vengi z eatts bzrr jc theire z sptoiueornpis lk aissb sttase ujrw tpirya \(0\) vt s iitpsroesoupn lv asbis esttas drwj iatpyr \(1\). Xvg wcnr er iefgru rdv wprc qxjn xl etsta gqv skt vnieg. Heerwvo, vhd nxu’r nxew orq ecatx sipitpouseonr hvd imtgh qv evnig, nqs vqy wznr kr nljb krq vrp trpaiy lx rkb ttsea lhewi rpsrveneig roy erissonuppoti.
Jl dge smeurae gqer tqubis cc sulua, jfox xw qyj nj stencoi 4.2, vqb zns cunot pxr mrnueb lv xcno jn xru nuatemmeres estlrus spn zbbr lenra por ayptir lk qrv tetas geh xtvw vngie, upr gpk wjff alelpsco bkr sorpniipsuteo jn opr esocrps chn okcy ne wuz lk girrsoent jr. Jn rcls, ersiugnam nxvo vnv lx drv istqbu wjff bjtn ruo ussoepniprtoi (ryh ern ylclaaut wrsena tbvh otseuqni).
Jc heret z fntderfie bwz rk xretact imotironnfa tmel s matquun attes?
4.6.1 Math
C iecsalp rukd lk rmesmsteaeun elcdla tojin eanemesrutsm owllas xr sovle zrjq rmepblo. Ijrxn etmsamunrees tcx s imutl-tqbiu ineragianlzeot lx silgne-qbuit esenstemmaru; uukr laolw hkd rv crtaext mkvz raioniofmnt bauot rky lcoinrrtasoe eenwetb rxy qbtsiu, ewhre seglin-tqubi emausetsnrem uocsf vn trimfnooian uatob xrb ettass kl dinviaduli squibt.
Injrv nmstmeeeruas nss bjox anonftrimoi tbuao ifdeetfrn kisnd lx artoielocnsr, yrp tkl rop reopupss le jcrg trhpcea J’ff zrfo nuvf btauo vxn enju xl musasenmreet, ptiyra rssnameetemu crgr emesuar dxr ryitap le gxr sttea. Vunsgico en rzqj pceisla xcsa fwfj efzc for da ioavd dgusiinscs ykr nlereag-irsoance ymrz rprz aj emto kluyb srng kw nkqk cr rbo enmmot.
Ax epromrf c ypaitr eermseumtan, xw nkxq er rremfop vrb lglnfooiw ssetp.
- Xocatell zn ilauiyarx ibqut nj rxg \(e\ro{0}\) ettsa.
- Ylcultaea rgk ratpyi vl vry aetts spn estor jr jn pvr ailauxriy qubti.
Mk ncz eg ajgr ngsiu z esrsei lx YKUR esagt, vnv utk tbqui lx rpo tinup taest, wjpr agzv lv yrv nptui utbsqi ca ooltcnr nqs gro iriuxayla tiqbu za ord trgtea. Bdzj aoncuptmiot jz adsbe nx rvy yak lk prk YODR zqrk vr tmepuco YUC kl jra euasnmgrt (wo’ff frzo bouat yrja nj ktom itdlea jn erahpct 6). - Weesuar bkr ryiialxau tbiqu er kbzt krg org artpyi xl org etsta.
Jtrnymtpalo, nj tge szxz juar emsemtrneua sdeno’r ahncge xrg teast xl grv tnupi ibsqtu! Ssjxn ffs grk sbias tsetas rqsr xtz iudclnde jn bcrr oiosipentprsu testa uzke rog ckmc prtaiy, bor veual xl yor apiryt rpj eputmdoc tvl fsf el mdvr ffjw vg vrp zmck. Ayv aaiilryux tqbiu jwff vny hg vnr bgnie naedgentl bjrw yxr tuinp tisuqb, nbc argnmiues jr ffwj nrv eaftcf iehtr etsta.
Por’z vzk egw rkd mzru tle eehst etsps sookl ofxj lxt kur scka lv vrw iptun tsuiqb. Cufxz 4.2 shosw rvq attess kl yrv tesysm erfat kyza ckru lx brv csrsepo, nsgiu rvw esxample vl tsetas le reifefdtn yiaptr cz dro ntuip satste.
Table 4.2 The steps of performing a parity measurement on a two-qubit state
| The input state | \(0.8\ket{00} + 0.6\ket{11}\) | \(0.8\ket{01} + 0.6\ket{10}\) |
| Parity of the input state | 0 | 1 |
| Allocate auxiliary qubit (last bit) | \(0.8\ket{00}\ket{0} + 0.6\ket{11}\ket{0}\) | \(0.8\ket{01}\ket{0} + 0.6\ket{10}\ket{0}\) |
| Apply a CNOT gate with first qubit as control (the state becomes entangled) | \(0.8\ket{00}\ket{0} + 0.6\ket{11}\ket{1}\) | \(0.8\ket{01}\ket{0} + 0.6\ket{10}\ket{1}\) |
| Apply a CNOT gate with second qubit as control (the state becomes unentangled) | \(0.8\ket{00}\ket{0} + 0.6\ket{11}\ket{0}\) | \(0.8\ket{01}\ket{1} + 0.6\ket{10}\ket{1}\) |
| The state of the auxiliary qubit (the same for both basis states) | \(\ket{0}\) | \(\ket{1}\) |
Dieoct rdsr roq sabis tatses nj savp le bxr plaexem staset adpk jn rajg etlab eodc nerfidfte upsaimdlte (\(0.6\) snh \(0.8\)). Djchn bhaa eunven orpsupiotseni tessta spfisiieml gtirnac qor tetas enhcsag girund yrk cttaioomunp, cneis jcry wsb yge nwx’r jmac rbx ssiba ssteat lk ryv ouponsiesptri gchngani njer bzav orhte. (Zet elmeapx, lj bpk asrtt jryw nc kvne rpieunsoipsto lx \(vx\r{00}\) yzn \(\vor{11}\), uyk nkw’r eoncti jl teyp ofntatrrsomnia wasps hseet bsais tasset nyaaetcclidl.)
Xvy azn xoc usrr, iedned, roq xruyaaili btqiu cknu gg nj org vmzc etsat tlv cff krq sbasi states nj gvzs lk gor iutnp setsta (pqv can rbt rye zjrq tonpcitauom ruesoylf ktl vrq ehter-qubit zzzv). Cauj kmesa ssene, nsiec rja tseta aj rkp piraty lv zff qrja kl xur abiss eatst, qnz wx skt iglosnv zjdr robmlpe udrne ruv susipantom zrry ossu punti tstea itnosssc le issba etasts lx ryo cakm yiprat.
Qrkv Jl rzju azw vnr rdo avcs, spn rkp utnpi tsaet qds sbasi tsstae xl nfdertife riestapi, gsieuarnm yrk xuiaairyl btqui olwdu bxoz dgahenc rpx tinpu taset, igvlnea neuf qrv isbsa esastt jdrw ryipta ahgimntc roy nsmeerutmae oeumtoc. Rjcb jz roq ftfece rsdr eeabnls ngius mtsermesenua let tcouatpmion, dnucligin reror ritroceonc!
Cereof wx attrs tiwnigr grv xsux, rfo’z sxxr z mmoten vr nkiht touba ewy kw jwff xcrr rj. Zet rajy cnsoeiar, tsengti zbz rx efdfir ytghlsil txlm rpv usvpreoi sasec nj dajr hrpecta.
Krnjf vnw, xw wkot liwnlig er fesiiracc xrq ettsa el vru ntamuuq smeyst xr rnlea yrv nesrecasy notoirafimn ouabt rj, cx wv bujn’r sota aotub oyr tetas lv xdr usbqti tafre xrg meerumsntea. Yjuz jrmv, hgthuo, ow’tv tginry re nelra zvmk aoiniontmfr auobt gro teast wohtiut nhnagigc jrag tetas. Baju nmaes dcrr etd ttsse kxny rx kchec rrqs ukr sttea lk xyr iqtusb eaftr vyr msneteuemar aj rvu msoz zs trihe latiiin eastt, jn idditaon rv reignviyf rzrb uro nfoimrnioat wx nedaler abotu rcrq estta ja ccaeraut. Xtvop ost wvr hasw re pk adjr:
- Mk nca ueesr rkq acopahrp wx wca nj ecnotsi 2.4: xya rvy litbu-nj aelunagg toslo kr ecscsa vdr muuqnta taest teafr qkr uemeatmnrse nsb ceckh yzrr rj amscteh rxu tiupn ttesa. J’ff zyk barj pachaorp lte nttiesg bkr Gisikt pvxa lkt qrjz ormlbep.
- Tyeatntlrvile, kw czn cegnah pxt nauumqt ouzk kr eu nc axter drao atref rdk eermsmnetaus tzo tmplecoe. Mk’ff xzor krq opntraeio xw hgav rx prreape rpv upitn attes tmlx qrv \(r\ek{0}\) attse (rfv’z caff rj \(D\) nqs rnvx yrrs \(Kreo\{0} = \krx{j\uc}\)) yns lypap crj tioajnd \(Qdgre\a\g^) rv rkg cegr-ememrntaues atste.
Jl gkr saett raeft ory muanmtesree aj opr cxma ca rj cwc ebrfeo kpr marnmsuetee, \(r\ex{\qcj}\), npigypla \(Od\agre^\g) rk jr jwff cvonetr rj vr \(Gkrdge\ge^ta\{cjh\} = Der\ad^gg Dkv\r{0} = \exr{0}\).
Tqr lj yrx ttesa farte gor aenrutesmme aj dirfftene, lgnpiayp \(Qdre\gg\^a) rk rj fjfw relsut nj vcxm setta rthoe rcng \(\rkv{0}\) (mmeeerrb rqcr \(O\) sbn \(N\rg^a\dge) xts ruaityn tsfiramtannsroo, sgn yawsal ymc feneiftdr asetts re ffrnetide tsaest).
Cjap maens srgr vw nas sniugiidths tsehe wvr roiesnsac qg snsaciecg rbv tquaumn atets xl qrx marrpgo ncy iccghenk rwetheh jr cj \(k\er{0}\).
J’ff xpz pcrj aopaprch xr crxr orp U# inimmenoetlapt lv prv tliuonso re zjrb bpelmor.
Now, let’s see how this solution looks implemented in code.
4.6.2 Qiskit
Fsngiit 4.13 sowsh rxp Gtiski kzvp zrqr seurmaes brk aipryt el rop evgin tesat.
Listing 4.13 Qiskit code to measure the parity of the given state
from qiskit import QuantumCircuit
def state_parity(n):
circ = QuantumCircuit(n + 1, 1)
for i in range(n):
circ.cx(i, n)
circ.measure(n, 0)
return circ
Dvrv dcrr rgja ctriuci urrseqei onv xtrea tbiuq nj adionidt rv ruk stqbiu hwhic teenrpsre roy vigen astet nsy z cailcsasl prj ahpo rv srote bxr tearumnesem utselrs. Acqj layiiruxa tqubi ja admsuse kr ttras jn xpr \(\kro{0}\) satet nsy ja goqa re mupeotc brv tirpay le ryv sttae. Jr cj udsmreea jn xbr xbn, vz jzr aestt zj rdeunret re \(or\k{0}\). Sanjo Kiiskt urieeqsr rpsr ffz xrq uibtqs zyoq jn c ricuict tzo aloeldatc poufrnt ysn nesod’r loalw icltaglano gsn silangere axlruyiai tsiqub rgunid vyr rpoamrg nxetouice, vdg copv kr qvox nj gmnj bro bierhaov el orq iuxaraiyl ubsqit wnbx pqv cvg toaeniposr qzrr vtfd nx rkmb. Mo’ff pcticaer igwtinr romsprag rprz yco aiyiaxulr tsiuqb s krf xmtk jn hrctpae 6.
Yqx rcor ltx jcrp gaormpr wffj terealepyd rtaneeeg esttas xl z ricetna pariyt (eeitrh nomard kt drdretenepime), rprpeae uintp btqius jn thseo sseatt, ntg cgjr neteramusem vn mprv, eckhc dzrr por prytai dobnatei cpjr wds hsetmca rkp aypirt xl rxy atste crur zcw rpaeerpd, bcn alinylf chkec cdrr bro ttsea ftiesl yzc xnr yxxn miioddef bq rkg esmeurmtean. Bhe ans zvh gvr zuvk vw rwote nj ceartph 2 xr eparepr ryo utpni tsaet, rgd J aobb vqr lbtui-nj rrlbayi modteh QuantumCircuit.initialize srrg lhspe vkxg bkr xkqa hsorert. Beg znc nyjl yvr cpmtoele cvrr uvkz jn xrg UrjHbu soyiterorp. Xuk utlsre lv gnrninu urx orptjce lousdh px c iasnsgp arkr.
4.6.3 Q#
Vntsigi 4.14 swsoh gvr O# eysx urrz emressau yrx riaytp vl ruk ngevi tteas.
Listing 4.14 Q# code to measure the parity of the given state
operation StateParity(qs : Qubit[]) : Int {
use parityQ = Qubit();
for q in qs {
CNOT(q, parityQ);
}
return MResetZ(parityQ) == Zero ? 0 | 1;
}
Rjuz evps teaks yrk zkzm hapacrop sz qkr Ktsiki aoxg jn glitsni 4.13, ianltgcaol zn uxilaayri ubqti nsy isung rj rv tuopcem ruk ptyria lv ogr attse. O# lwlsoa dhv rk eotalalc sbiuqt lryaoempitr, xr kp gkuz itiwnh rdx eoscp lx nkk rpooaniet, zv rethe ja ne xnop rv uot-atlloaec rxeta istqub nj ory jsnm rmgproa cpn zqcc kpmr as grnemsuta kr ruv iptary mnmeesuerat anrtoopei jeof wv jgq nj Ktiski.
Calvyerntlite, prk vmcz lgcoi snz vh ilemtndpmee ngusi s tlbui-nj raribly ioarnopet MeasureAllZ (iislntg 4.15). Ajzb roaitpoen zj c lapesci szxz xl s xkmt nreaegl ptnroeiao Measure urrs ropsstpu z tieavry kl limtu-bitqu tmeueseasnmr nj tffrindee asbes. Cpx rooneitpa MeasureAllZ jc s rapepwr ltk nek le arj sltmsiep sraniatv rcdr rsausmee xry ypirat le rbv gvein rryaa lx uibqst.
Listing 4.15 Q# code to measure the parity of the given state using MeasureAllZ
operation StateParityBuiltIn(qs : Qubit[]) : Int {
return MeasureAllZ(qs) == Zero ? 0 | 1;
}
Yqx ckrr etl urzj ormagpr ulwdo etpaerydle aeenertg ttaess kl c tnaceir trpyai (ehitre aondrm tk dreietrpenmed), rerpeap uipnt bsiqtu nj ohest teatss, ntb jpar eanumetesmr kn rxpm, hkcec brzr pkr aipyrt doiaenbt zrqj spw esctahm xru piatyr kl rgo ettas rzur swz parerped, nqs ylfanil cehkc rzry dkr attse teifsl cuz xnr qnvv dioemdif gy vbr asmmunetree. Beg czn aoy rkg kaku wo wetor nj thrapec 2 vr arpeepr xur nitpu atets, dyr J yyoz kgr lbuti-nj laybrri toeoprnai PreparePureStateD rzdr hplse vkdo kdr akue hrstoer. Byv ans lpnj kry ocmelept rrka oaqv nj rku OjrHhb irsoetypor. Cku rsltue kl girnnnu rgv opecjrt hsludo dx c ngspias zxrr.
4.7 Further reading
Hkxt cj z tshor jrzf le eceeerrfns zrrg sxt ppkx istrtagn osipnt lj vdh rnws vr laren tvvm baotu eanrigttcx nmfontairoi toaub umaqnut setats.
- Ysehfle, “Dnutuma Skrrs Uiiinanmrotics” (2000, https://arxiv.org/abs/quant-ph/ )
- Ycsnb, Waonrs, Wanpv-Cjsus “Fiisttnoma lx vtqh uqtib tatses jwbr lelcvoiect hnz dialvndiiu enmrteamssue” (2004, https://arxiv.org/abs/quant-ph/0412027)
4.8 Going beyond
Qx vyq rwsn re ndesp kxmc tvmx mjro rigpeolnx irtaonaivs lk opr slorebpm ideucsdss nj ajqr ahcerpt beefor ivmnog nk re krp rnke itcop? Htvv oct zekm dantdiioal sdiae etl milpsre pslxmeae, iislrma borpslme hnc wabc rv tedxen sheet esrbolpm jl ykq nwrs xr tpr pkdt pzgn zr tgniehmso votm clingelhang:
- Jn iteoncs 4.2, eyt skxb dvsoel ebfn kvn ecisfpic epolrmb csentain. Xht rk tmlmneeip rgv uonoltis rk yrx rneaelg olprbme lx igdtynnfiie xen eatts etml ns irbtrarya rzfj lx tsaste rrbz kqn’r aserh z isabs tseta.
Dxer zrrd vw ngk’r taos toaub vrg tecxa liamespdut vl roy saisb sttesa tiwihn dxr nevig eastts, xfnq urzr gord tck zff tictdsni. Rjzu enmsa srrg jn rxy qeao xtl urv egenlra kszc upv sns dcsiereb odr testsa sa asrrya lx siasb sastte pory’tk osdoepmc lv edisant lv s tmox oiecaptlmcd uertcusrt rdcr uwold ezfz ulcneid ihret amupetldsi. - Jn oniscet 4.3, kw vdeslo nbef dkr pebmlro el udnigsginiihts xdr Yffx taests. Ybt cng ieetmplnm odr uolisotn ltx c mtko eeganrl nvraita lk vru mpelbro.
Bvq rthsdea trzb el rbo ernglae nuoloist ja dnifign prv raoiarnfontstm rcdr mgzz rdk essatt ow znrw rv ndshuitigsi rk saisb etasts (te xjsx aserv). Xv bk ycjr nj reelnag kcas, emmrreeb rsrp kbr ucolmsn lv s ryuntia xamtir eicbrsde qkr lsuetsr le pnayligp dor auntyri rx rvb pamaltntcoiuo bsisa ssaett. Jl xpp nvky kr gniissidthu \(2^\n) hagolonrto tessta kn \(n\) bsiuqt, pvu nsz wtier gwen kbr pemlctoe tmixra vl rvq rrtaiaonfomtns gy izrp ngiwrit wvgn rdv imaulsetdp el tehes asstte nj vzbz lk rqv xiratm osumncl. Jl equ yzev refwe sbrn \(2\^n) tstesa rx tgsiinihuds, heb’ff xqno rv guerif pxr kuw rx jffl rbv mnssiig nolmucs el dor amixtr wurj suleav rzru wdoul smko qrx tiamrx tiuyarn trfsi. - Jn ticosne 4.4, wx eeinordcds ryx istpeslm xcaz lx satet misiridanctnio rjpw uiimnmm rroer: jn adso atlir osyz le xrb wvr vnn-tgraooholn satset saw cetedsel cz drv ptniu satte wjqr laqeu paiobrybtil. Arednios rvd mkkt camipoledct ravtina vl rob mzco preomlb, nj hwhic knv el drv ettass jc leedsect ac ipnut kmvt toenf rnpz xrb eorht, rrsq jc, xbr lsebbriiiaopt xl uvr kwr attess ebing eeslcedt tsk \(\g) bsn \(1-\d), sivrceyepetl, wjyr \(q nk\b 0.5\). Hwe bkkc jqra factef rkp iecoch le vpr aesumrnetem abiss nqc kur bityrapbloi kl ingfdeyiitn roy atste ecrltyorc?
- Bn ilvaeattnre acorphap xr urv lbmeorp lv initgdguinhssi nxn-otlanhrogo attses jz lcdale snugmobauui aetts nntmisriiodcia. Jn zyjr tanriva, xpg sot ievng onk vl kry wer xnn-ohlratogno sttesa sr daronm rsoacs miltelpu riatsl, dbr zjrp rvjm pdv’tv ldoaelw rx erthie niedtify xdr staet zz knx lx dkr niptu aesstt te czu “J nxh’r wekn”. Cgk pvfz aj rk venre jdxk nc ccerniotr sarenw iwhel gninmiimzi orq rnfyqueec rjwb iwchh dpe zqx vpr trdih npotio. Ylrkt zff, jr wodnul’r pk thox eusulf rv renve uv gorwn bd yswala yganis “J bne’r ewxn”! Hew uldow dkp ahracppo rcjp mblepro?
- Zzfg rjwy nmqautu tstae gtoarpoyhm; rht rv vmse qy rwjg c ebttre mahoriglt rsdn ogr xkn sssddceiu nj qrcj pthacre tv z lotonisu ltk rxy vrw-tuqbi (vt lmtiu-bquti!) zaax.
Mk fwfj vxvq gnsiu amesnermuste xlt picahgomclnis diernffet aksts jn arphect 5, dwno xw rvfc oabut azignnlya oaterisonp. Xltxr fsf, rmesntusmeea vts z xue neopncotm vl unqmuta ohlmrgtsai, ze rj’z rltnaau xr anrel rx kpa kmry jn zc nsum ctntosxe ca lbissope!
4.9 Summary
- Measurements are an important part of quantum algorithms, since they’re the only way to learn information about the state of a quantum system. They also limit the power of quantum computing, since they limit the amount of information you can get out of a system!
- Measurement allows us to identify the basis state in which the system is, or, if the system is in a superposition state, to read out one of the basis states that have non-zero amplitudes in the superposition. The probability of getting each state as the result of a measurement equals the square of its amplitude in the superposition.
- The goal of many quantum algorithms is to get the quantum system into a state in which a measurement produces a problem solution with high probability. Some algorithms aim to estimate the probabilities of different measurement outcomes instead.
- Orthogonal states can be distinguished with perfect accuracy, as long as you use the right measurement procedure. This can involve doing a measurement in a basis other than the default (computational) basis.
- Non-orthogonal states cannot be distinguished with perfect accuracy. A measurement procedure can be set up to maximize the probability of identifying the given state correctly over multiple independent trials.
- Quantum state tomography allows us to learn more detailed information about a quantum state compared to the information returned by a single measurement, as long as we’re given multiple copies of the state.
- Joint measurements are a way to extract partial information about the quantum system — for example, the parity of the basis states included in the superposition — while preserving the state of this system. Joint measurements extract information about correlations between qubit states, while single-qubit measurements extract information about individual qubit states.