Appendix C. A primer on linear algebra
This appendix presents the basic linear algebra operations. They’re important for understanding much of the math behind most machine-learning algorithms. In case you skipped your linear algebra classes, this is your chance to come to grips with it.
A matrix is a set of elements arranged in rows and columns (we’ll only use matrices whose elements are numbers). This is a matrix with two rows and three columns, so it’s called a 2 × 3 matrix:
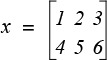
Usually, the number of rows in a matrix is denoted by the letter m and the number of columns by the letter n. m and n are the matrix’s dimensions, and we say its size is m × n. We’ll denote matrices with bold, uppercase letters (X in the previous example) and its elements with plain, lowercase letters with subscript indices. For example:
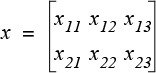
A column vector is a matrix of size n × 1, and a row vector is a matrix of size 1 × n. We’ll refer to column vectors with lowercase, italic, bold letters (for example, u) and row vectors just like column vectors, but with an added superscript letter T (for example, uT):

The letter T here means transposed. Transposition is an operation in which the rows of a matrix become its columns, and vice versa. For our example matrix X, its transposed matrix would be as follows:
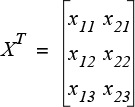
So, if the size of the original matrix is m × n, the size of the transposed matrix will be n × m. Note that (XT)T = X.