1 Small problems
To get started, we will explore some simple problems that can be solved with no more than a few relatively short functions. Although these problems are small, they will still allow us to explore some interesting problem-solving techniques. Think of them as a good warm-up.
1.1 The Fibonacci sequence
The Fibonacci sequence is a sequence of numbers such that any number, except for the first and second, is the sum of the previous two:
0, 1, 1, 2, 3, 5, 8, 13, 21...
The value of the first Fibonacci number in the sequence is 0. The value of the fourth Fibonacci number is 2. It follows that to get the value of any Fibonacci number, n, in the sequence, one can use the formula
fib(n) = fib(n - 1) + fib(n - 2)
1.1.1 A first recursive attempt
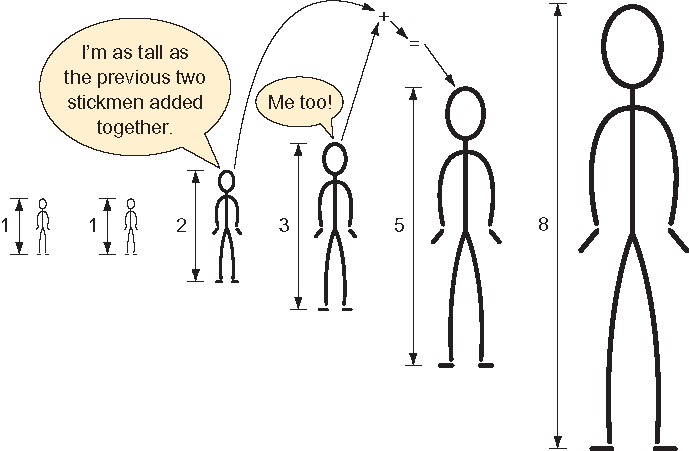
The preceding formula for computing a number in the Fibonacci sequence (illustrated in figure 1.1) is a form of pseudocode that can be trivially translated into a recursive Java method. (A recursive method is a method that calls itself.) This mechanical translation will serve as our first attempt at writing a method to return a given value of the Fibonacci sequence.
Listing 1.1 Fib1.java
package chapter1;
public class Fib1 {
// This method will cause a java.lang.StackOverflowError
private static int fib1(int n) {
return fib1(n - 1) + fib1(n - 2);
}
Figure 1.1 The height of each stickman is the previous two stickmen’s heights added together.
Let’s try to run this method by calling it with a value.