14 An Introduction to Graphs
Finding Paths of Minimum Distance
This chapter covers
- Briefly introducing graphs from a theoretical point of view
- Strategies to implement graphs
- Formulating a problem: finding the best route for deliveries
- Search algorithms on graphs: BFS, DFS
- Using BFS to find the route that traverses the fewest blocks
- Minimum distance algorithms: Dijkstra – finding the shortest route
- Optimal search: A* algorithm (reading “A-star”) – finding the quickest route
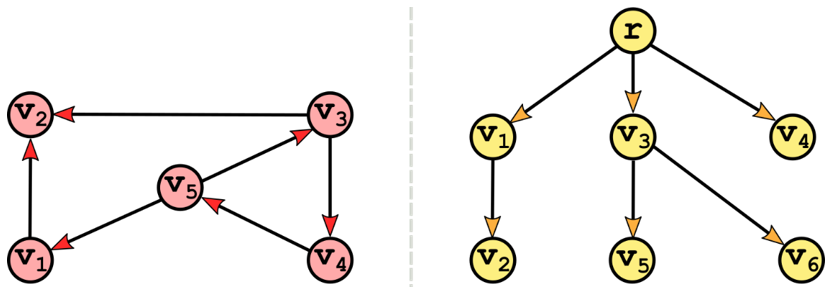
We have already described the basics of trees in appendix C, and used several kinds of trees in the previous chapters: binary search trees, heaps, k-d trees etc...: you should be now familiar with them. Graphs could be considered a generalization of tree, although in reality the opposite is true, and it is trees that are a special case of graphs: a tree, in fact, is a connected, acyclic undirected graph. Figure 14.1 shows an example of two graphs, only one of which is a tree: don’t worry if you are not sure which one, in this chapter we’ll take a closer look at the meaning of those properties in the definition of trees, and they will help us explain graphs’ properties better, and make sense of these examples.
But to do so we need to follow a meaningful order and so, before that, we need to give a formal definition of graphs, and understand how we can represent them.
Figure 14.1 Two graphs, only one of which is also a tree: can you tell which one?